Cho hình chóp tứ giác đều có cạnh đáy bằng x. Diện tích xung quanh gấp đôi diện tích đáy. Khi đó thể tích khối chóp bằng:
A. 3 12 x 3
B. 3 2 x 3
C. 3 3 x 3
D. 3 6 x 3
Đáp án là D
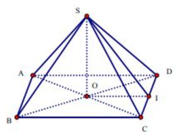
Thể tích khối chóp
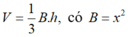
Gọi O là tâm của hình vuông, I là trung điểm DC thì SI ⊥ CD .
Đặt SO = h. Có
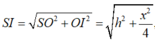
Suy ra:
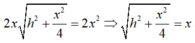
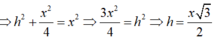
Lúc đó:
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều có cạnh đáy bằng x . Diện tích xung quanh gấp đôi diện tích đáy. Khi đó thể tích khối chóp bằng: A.
3
12
x
3
.
B.
3
2
x
3
.
C.
3
3
x
3
....
Đọc tiếp
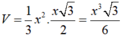
Cho hình chóp tứ giác đều có cạnh đáy bằng x . Diện tích xung quanh gấp đôi diện tích đáy. Khi đó thể tích khối chóp bằng:
A. 3 12 x 3 .
B. 3 2 x 3 .
C. 3 3 x 3 .
D. 3 6 x 3 .
Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Thể tích của khối chóp đã cho bằng A.
a
3
3
2
B.
a
3
3
3
C.
a
3...
Đọc tiếp
Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Thể tích của khối chóp đã cho bằng
A. a 3 3 2
B. a 3 3 3
C. a 3 3 6
D. a 3 3 12
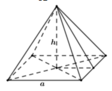
Gọi chiều cao của hình chớp là h. Khi đó ta tính được diện tích xung quanh của hình chóp là 
Theo yêu cầu bài toán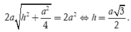 
Thể tích khối chóp là: 
Chọn C.
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của khối chóp.
Đọc tiếp
Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của khối chóp.
Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của khối chóp. A.
V
a
3
3
2
B.
V
a
3
3
3
C.
V
a...
Đọc tiếp
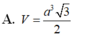
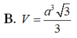
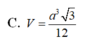
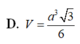
Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của khối chóp.
A. V = a 3 3 2
B. V = a 3 3 3
C. V = a 3 3 12
D. V = a 3 3 6
Đáp án D.
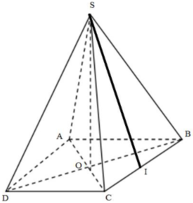
Phương pháp:
+) Gọi b là độ dài cạnh bên, sử dụng giả thiết diện tích xung quanh gấp đôi diện tích đáy biểu diễn b theo a.
+) Gọi O = AC ∩ BD ⇒ SO ⊥ (ABCD)
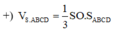
Cách giải:
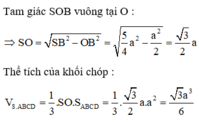
Gọi b là độ dài cạnh bên, I là trung điểm của BC ⇒ SI ⊥ BC
Tam giác SIB vuông tại I
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của khối chóp. A.
V
a
3
3
2
B.
V
a
3
3
3
C.
V
a...
Đọc tiếp
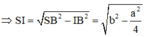
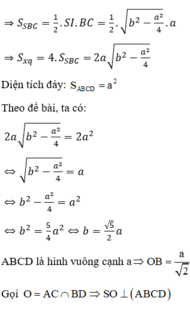
Cho hình chóp tứ giác đều có cạnh đáy bằng a và biết diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của khối chóp.
A. V = a 3 3 2
B. V = a 3 3 3
C. V = a 3 3 12
D. V = a 3 3 6
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD. Khi đó diện tích xung quanh và thể tích của hình nón bằng A.
S
xq
πa
2
;
V
πa
3...
Đọc tiếp
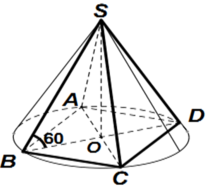
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD. Khi đó diện tích xung quanh và thể tích của hình nón bằng
A. S xq = πa 2 ; V = πa 3 6 12
B. S xq = πa 2 ; V = πa 3 3 12
C. S xq = 2 πa 2 ; V = πa 3 3 12
D. S xq = 2 πa 2 ; V = πa 3 6 6
Đáp án A
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
Đúng 0
Bình luận (0)
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 21:50
Thể tích của khối chóp cụt tam giác đều có cạnh đáy lớn bằng \(2a\), cạnh đáy nhỏ bằng \(a\) và chiều cao bằng \(\frac{{a\sqrt 6 }}{3}\) là
A. \(\frac{{7\sqrt 2 }}{8}{a^3}\).
B. \(\frac{{\sqrt 2 }}{4}{a^3}\).
C. \(\frac{{7\sqrt 2 }}{{12}}{a^3}\).
D. \(\frac{{7\sqrt 3 }}{4}{a^3}\).
Diện tích đáy lớn là: \(S = \frac{{{{\left( {2{\rm{a}}} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Diện tích đáy bé là: \(S' = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích của bồn chứa là: \(V = \frac{1}{3}.\frac{{a\sqrt 6 }}{3}\left( {{a^2}\sqrt 3 + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} + \frac{{{a^2}\sqrt 3 }}{4}} \right) = \frac{{7\sqrt 2 }}{{12}}{a^3}\)
Chọn C.
Đúng 0
Bình luận (0)
Một hình chóp tứ giác đều có cạnh đáy bằng 10dm . Biết số đo diện tích xung quanh ( đơn vị dm2) bằng số đo cuả thể tích (đơn vị dm3). Tính chiều cao , diện tích xung quanh và thể tích của hình chóp.
một hình chóp tứ giác đều có chiều cao bằng 15cm, trung đoạn bằng 17cm, độ dài cạnh đáy của hình chóp bằng 16cm. Tính diện tích xung quanh, diện tích toàn phần ( tổng diện tích các mặt đáy của hình chóp ), thể tích của hình chóp tứ giác đều?
Sxq=16*4*17/2=544cm2
Stp=544+16^2=800cm2
V=1/3*16^2*15=1280cm3
Đúng 0
Bình luận (0)
Nữa chu vi đáy của hình chóp đều:
\(16\cdot4:2=32\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=32\cdot17=544\left(cm^2\right)\)
Diện tích mặt đáy của hình chóp đều:
\(S_đ=16^2=256\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=544+256=800\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot256\cdot15=1280\left(cm^3\right)\)
Đúng 0
Bình luận (0)