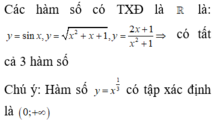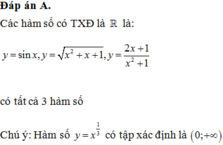\(x^2-\left(m+2\right)x+m=0\left(1\right)\)

Để phương trình (1) có nghiệm thì:

\(\Delta\ge0\Rightarrow\left(m+2\right)^2-4m\ge0\)

\(\Leftrightarrow m^2+4\ge0\) (luôn đúng)

Vậy \(\forall m\) thì phương trình (1) luôn có nghiệm.

Theo định lí Viete cho phương trình (1) ta có:

\(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=m\end{matrix}\right.\)

\(A=x_1^3-\left(m+1\right)x_1^2+mx_1-5m\)

\(=x_1^3-\left(x_1+x_2-1\right)x_1^2+x_1\left(m-5\right)\)

\(=x_1^3-x_1^3-x_1^2x_2+x_1^2+x_1\left(x_1x_2-5\right)\)

\(=-x_1^2x_2+x_1^2+x_1^2x_2-5x_1\)

\(=x_1^2-5x_1=\left(x_1^2-5x_1+\dfrac{25}{4}\right)-\dfrac{25}{4}=\left(x_1-\dfrac{5}{2}\right)^2-\dfrac{25}{4}\ge-\dfrac{25}{4}\)

Vậy \(MinA=-\dfrac{25}{4}\).

a)

Xét x=0 => A = 1 không là số nguyên tố

Xét x=1 => A= 3 là số nguyên tố (chọn)

Xét x>1

Có A = x14+ x13 + 1 = x14 - x2 + x13 - x + x2 + x + 1

A = x2(x12-1) + x(x12-1) + x2+x+1

A = (x2+x)(x3*4-1) + x2 + x + 1

Có x3*4 chia hết cho x3

=> x3*4-1 chia hết cho x3 - 1 = (x-1)(x2+x+1)

=> x3*4-1 chia hết cho x2+x+1

=>A chia hết cho x2+x+1 mà x2+x+1 >0 (do x>1)

=> A là hợp số với mọi x > 1 (do A chia hết cho x2+x+1)

Vậy x=1 để...

Ta có: \(26\times8+4\times13-10\times26\)

\(=13\times2\times8+4\times13-10\times2\times13\)

\(=13\times16+4\times13-20\times13\)

\(=13\times\left(16+4-20\right)=13\times0=0\)

26 x 8 + 4 x 13 - 10 x 26

= 13 x 2 x 8 + 4 x 13 - 10 x 2 x 13

= 13 x 16 + 4 x 13 - 20 x 13

= 13 x ( 16 + 4 - 20)

= 13 x 0

= 0

26 x 8 + 4 x13 - 10 x 26 

=13 * 2 * 8 + 4 * 13 - 10 * 2* 13

=13 * 16 + 4 *13 -20 *13

=13 * (16 + 4 - 20)

=13 * 0

=0

\(a,\dfrac{5}{13}\times\dfrac{4}{15}\times13=\dfrac{5\times4\times13}{13\times5\times3}=\dfrac{4}{3}\\ b,\left(\dfrac{3}{7}+\dfrac{5}{2}\right)\times\dfrac{7}{5}=\dfrac{3}{7}\times\dfrac{7}{5}+\dfrac{5}{2}\times\dfrac{7}{5}=\dfrac{3}{5}+\dfrac{7}{2}=\dfrac{6}{10}+\dfrac{35}{10}=\dfrac{41}{10}\\ c,\dfrac{1}{5}\times\dfrac{11}{18}+\dfrac{11}{18}\times\dfrac{3}{5}=\dfrac{11}{18}\times\left(\dfrac{1}{5}+\dfrac{3}{5}\right)=\dfrac{11}{18}\times\dfrac{4}{5}=\dfrac{22}{45}\)

a, 4/3  b, 41/10   c,22/45

=\(12.1.3.6\)

=\(12.3.6\)

=\(36.6\)

=\(216\)

\(^ofer\)

Đề có nhầm ko bạn

\(=\)\(\dfrac{13}{x-1}+\dfrac{5}{2(x-1)}-\dfrac{2}{(x-1)}\)\(\)

\(=\)\(\dfrac{26+5-4}{2(x-1)}\)

\(=\)\(\dfrac{27}{2(x-1)}\)

a)

3. x 13 = 45 − 26 . − 2 5 3. x 13 = 9 13 3. x = 9 x = 3

b)

13 21 − 3 2 . 21 13 + x = 4 13 − 27 42 . 21 13 + x = 4 13 − 27 26 + x = 4 13 x = 4 13 − − 27 26 x = 35 26

Đáp án đúng : A