Phương trình sin2x+3cosx = 0 có bao nhiêu nghiệm trong khoảng 0 ; π
A. 0
B. 1
C. 2
D. 3
Phương trình sin2x+3cosx=0 có bao nhiêu nghiệm trong khoảng 0 ; π ?
A. 0
B. 1
C. 2
D. 3
Phương trình sin 2 x = − 2 2 có bao nhiêu nghiệm thuộc khoảng 0 ; π ?
A. 4
B. 3
C. 2
D. 1
Đáp án C
PT 2 x = − π 4 + k 2 π 2 x = 5 π 4 + k 2 π ⇔ x = − π 8 + k π x = 5 π 8 + k π k ∈ ℤ
Vì x ∈ 0 ; π ⇒ 0 < − π 8 + k π < π 0 < 5 π 8 + k π < π ⇔ 1 8 < k < 9 8 − 5 8 < k < 3 8 ⇒ k = 1 k = 0 ⇒ x = 7 π 8 x = 5 π 8
Cho phương trình
tan x + 1 3 sin x + 2 cos = m sin x + 3 cos x .
Có bao nhiêu giá trị nguyên của tham số m ∈ 0 ; 2019 để phương trình có đúng một nghiệm thuộc khoảng 0 ; π 2
A. 2017
B. 2018
C. 2019
D. 2020
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4 cos 3 x - cos 2 x + m - 3 cos x - 1 = 0 có đúng bốn nghiệm khác nhau thuộc khoảng - π 2 ; π 2
A. 2
B. 3
C. 0
D. 1
Phương trình sin 2 x + cos x = 0 có tổng các nghiệm trong khoảng 0 ; 2 π bằng
A. 2 π
B. 3 π
C. 5 π
D. 6 π
Đáp án là C.
p t ⇔ cos x 2 sin x + 1 = 0 ⇔ cos x = 0 sin x = − 1 2 ⇔ x = π 2 + k π x = − π 6 + k 2 π x = 7 π 6 + k 2 π ; k ∈ ℤ
x ∈ 0 ; 2 π ⇒ x ∈ π 2 ; 3 π 2 ; − π 6 ; 7 π 6 .
Tổng các nghiệm 5 π
Số nghiệm của phương trình: \(sin2x+\sqrt{3}cos2x=\sqrt{3}\) trên khoảng \(\left(0;\dfrac{\pi}{2}\right)\)là bao nhiêu ?
Pt \(\Leftrightarrow2sin\left(2x+\dfrac{\pi}{3}\right)=\sqrt{3}\)
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(x\in\left(0;\dfrac{\pi}{2}\right)\)\(\Rightarrow\left[{}\begin{matrix}0< \dfrac{\pi}{6}+k\pi< \dfrac{\pi}{2}\\0< k\pi< \dfrac{\pi}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{1}{6}< k< \dfrac{1}{3}\\0< k< \dfrac{1}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)\(\Leftrightarrow\left[{}\begin{matrix}k=0\\k\in\varnothing\end{matrix}\right.\)
Vậy có 1 nghiệm thỏa mãn
Phương trình s i n 2 3 x . c o s 2 x + s i n 2 x = 0 có bao nhiêu nghiệm thuộc (0;2017).
A. 2016
B. 1003
C. 1284
D. 1283
Phương trình sin 2 x = − 1 2 có bao nhiêu nghiệm thỏa 0 < x < π
A. 1
B. 3
C. 2
D. 4
Đáp án C
Ta có sin 2 x = − 1 2 ⇔ sin 2 x = sin − π 6
⇔ 2 x = − π 6 + k 2 π 2 x = π + π 6 + k 2 π ⇔ x = − π 12 + k π x = 7 π 12 + k π k ∈ ℤ
Trường hợp 1: x = − π 12 + k π .Do 0 < x < π nên 0 < π 12 + k π < π ⇔ 1 12 < k < 13 12
Vì k ∈ ℤ nên ta chọn được k = 1 thỏa mãn. Do đó, ta được nghiệm x = 11 π 12 .
Trường hợp 2: x = 7 π 12 + k π . Do 0 < x < π nên 0 < 7 π 12 + k π < π ⇔ − 7 12 < k < 5 12
Vì k ∈ ℤ nên ta chọn được k = 0 thỏa mãn. Do đó, ta được nghiệm x = 7 π 12 .
Vậy phương trình đã cho có hai nghiệm.
Có bao nhiêu nghiệm của phương trình sin 2 x - sin x = 0 thỏa mãn điều kiện 0 < x < π
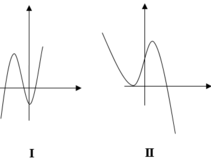
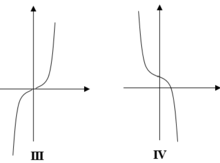
A. Đồ thị (III) xảy ra khi
B. Đồ thị (IV) xảy ra khi
C. Đồ thị (II) xảy ra khi
D. Đồ thị (I) xảy ra khi