Cho một đa giác đều 2n đỉnh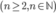 
Tìm n biết số hình chữ nhật được tạo ra từ bốn đỉnh trong số 2n đỉnh của đa giác đó là 45
A. n = 12
B. n = 10
C. n = 9
D. n = 45
Đáp án B
Đa giác đều 2n đỉnh có n đường chéo qua tâm. Cứ 2 đường chéo qua tâm tương ứng với 1 hình chữ nhật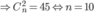 
Cho đa giác đều A 1 A 2 . .. A 2 n n ≥ 2 , n ∈ Z nội tiếp đường tròn O. Biết rằng số tam giác trong 2n điểm A 1 , A 2 , . .. , A 2 n gấp 20 lần số hình chữ nhật có 4 đỉnh trong 2n điểm đó. Tìm n.
A. 12
B. 8
C. 16
D. 10
Cho đa giác đều 2n đỉnh n ≥ 2 . Hỏi có bao nhiêu hình chữ nhật có 4 đỉnh là 4 trong 2n đỉnh của đa giác.
A. C 2 n 2
B. C n 4
C. C 2 n 4
D. C n 2
Đáp án D
Đa giác đều 2n đỉnh có n đường chéo qua tâm. Cứ 2 đường chéo qua tâm tương ứng với 1 hình chữ nhật có 4 đỉnh là đỉnh của đa giác. Do đó số hình chữ nhật là C n 2
Cho đa giác đều A1A2…A2n nội tiếp trong đường tròn tâm O. Biết rằng số tam giác có đỉnh là 3 trong 2n điểm A1;A2;…;A2n gấp 20 lần so với số hình chữ nhật có đỉnh là 4 trong 2n điểm A1;A2;…;A2n . Tìm n?
A. 3
B. 6
C.8
D.12
Số tam giác có các đỉnh là 3 trong 2n điểm A1;A2;…;A2n là: 
Ta thấy ứng với hai đường chéo đi qua tâm O của đa giác A1A2…A2n cho tương ứng một hình chữ nhật có 4 đỉnh là 4 điểm trong 2n điểm A1;A2;…;A2n và ngược lại mỗi hình chữ nhật như vậy sẽ cho tương ứng hai đường chéo đi qua tâm O của đa giác.
Mà số đường chéo đi qua tâm của đa giác là n nên số hình chữ nhật có đỉnh là 4 trong 2n điểm bằng 
Theo giả thiết: 
⇒n=8.
Chọn C
Cho đa giác đều \(A_1A_2.....A_n,\) (\(n\ge2\), n nguyên) nội tiếp đường tròn O. Biết rằng số tam giác có 3 đỉnh trong 2 n điểm \(A_1,A_2,....,.A_{2n}\) gấp 20 lần số hình chữ nhật có 4 đỉnh trong 2n điểm \(A_1A_2.....A_n\). Tìm n
Số tam giác là \(C_{2n}^3\). Một đa giác đều 2n đỉnh thì có n đường chéo xuyên tâm. Cứ 2 đường chéo xuyên tâm thì có một hình chữ nhật theo yêu cầu. Vậy số hình chữ nhật là \(C_n^2\).
Theo bài ta có phương trình :
\(C_{2n}^3=20C_n^2,\left(n\ge2\right)\)
\(\Leftrightarrow\frac{\left(2n\right)!}{\left(2n-3\right)!3!}=20\frac{n!}{\left(n-2\right)!2!}\)
\(\Leftrightarrow\frac{\left(2n-2\right)\left(2n-1\right)2n}{3}=20\left(n-1\right)n\)
\(\Leftrightarrow2\left(n-1\right)\left(2n-1\right)2n=60\left(n-1\right)n\)
\(\Leftrightarrow2n-1=15\), (do \(n\ge2\))
\(\Leftrightarrow n=18\)
Vậy đa giác đều có 16 cạnh, (thập lục giác đều)
Cho một đa giác đều gồm 2n đỉnh n ≥ 2 , n ∈ ℕ . Chọn ngẫu nhiên ba đỉnh trong số 2n đỉnh của đa giác, xác suất ba đỉnh được chọn tạo thành một tam giác vuông là 1/5. Tìm n .
A. 5
B. 4
C. 10
D. 8
Đáp án D
Số tam giác tạo thành khi chọn ngẫu nhiên 3 điểm là: C 2 n 3
Số đường chéo đi qua tâm là n ⇒ số hình chữ nhật nhận 2 đường chéo đi qua tâm làm 2 đường chéo là: C n 2
Số tam giác vuông được tạo thành là 4 C n 2
Ta có: 4 C n 2 C 2 n 3 = 1 5 ⇒ n = 8.
Cho một đa giác đều gồm 2n đỉnh ( n ≥ 2 , n ∈ ℕ ) . Chọn ngẫu nhiên ba đỉnh trong số 2n đỉnh của đa giác, xác suất ba đỉnh được chọn tạo thành một tam giác vuông là 1 5 . Tìm n.
A. n = 5
B. n = 4
C. n = 10
D. n = 8
Đáp án D
Số tam giác tạo thành khi chọn ngẫu nhiên 3 điểm là: C 2 n 3
Số đường chéo đi qua tâm là n => số hình chữ nhật nhận 2 đường chéo đi qua tâm làm 2 đường chéo là: C n 2 .
Số tam giác vuông được tạo thành là: 4 . C n 2 .
Ta có: 4 C n 2 C 2 n 3 = 1 5 ⇒ n = 1 8 .
Cho đa giác đều \(A_1A_2...A_{2n}\left(n\ge2,n\in N\right).\) Biết rằng số vecto khác vecto 0 có điểm đầu và điểm cuối thuộc tập hợp điểm \(\left\{A_1,A_2,...,A_{2n}\right\}\) bằng 9 lần số hình chữ nhật có các đỉnh thuộc tập hợp điểm \(\left\{A_1,A_2,...,A_{2n}\right\}\). Tìm n
Số vecto tạo từ 2n điểm là: \(A_{2n}^2\)
Đa giác đều 2n đỉnh có n đường chéo, cứ 2 đường chéo cho ta 1 hình chữ nhật tương ứng, do đó số hình chữ nhật có đỉnh là đỉnh của đa giác đều là: \(C_n^2\)
\(\Rightarrow A_{2n}^2=9C_n^2\Leftrightarrow\dfrac{\left(2n\right)!}{\left(2n-2\right)!}=\dfrac{9.n!}{2!.\left(n-2\right)!}\)
\(\Leftrightarrow2n\left(2n-1\right)=\dfrac{9n\left(n-1\right)}{2}\)
\(\Leftrightarrow n=5\)
Cho một đa giác đều gồm 2n đỉnh (n≥2, nÎN*). Chọn ngẫu nhiên ba đỉnh trong sổ 2n đỉnh của đa giác, xác suất ba đỉnh được chọn tạo thành một tam giác vuông là 1 5 . Tìm n.
A. 5
B. 4
C. 10
D. 8
Gọi A là biến cố để 3 đỉnh tạo thành một tam giác vuông.
Ta có một đa giác đều 2n cạnh có n đường chéo đi qua tâm.
Ta lấy hai đường chéo thì tạo thành một hình chữ nhật.
Mỗi một hình chữ nhật sẽ có bốn tam giác vuông.
Vậy số tam giác vuông tạo thành từ đa giác đều 2n đỉnh là
