Thể tích của một khối cầu có bán kính R là
A. V = 4 3 π R 3
B. V = 1 3 π R 3
C. V = 4 3 π R 2
D. V = 4 π R 3
Khối lượng riêng của thép là \(7850kg\)/m3. Tính khối lượng của một quả cầu thép bán kính 0,15 m. Cho biết công thức tính thể tích của khối cầu là \(V=\dfrac{4}{3}\pi r^3\), với r là bán kính quả cầu.
Thể tích của quả cầu thép là:
\(V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi .0,{15^3} = 0,014\left( {{m^3}} \right)\)
Khối lượng của quả cầu thép là:
\(m = \rho V = 7850.0,014 = 110\left( {kg} \right)\)
Cho một mặt cầu có diện tích S, thể tích khối cầu đó là V. Bán kính R của mặt cầu là:
A. R = 4V/S B. R = S/3V
C. R = 3V/S D. R = V/3S
Chọn C.
Dựa vào công thức diện tích mặt cầu và thể tích hình cầu, ta có:
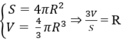
Khối lượng riêng của thép là 7850kg/m3. Tính khối lượng của một quả cầu thép bán kính 0,15 m. Cho biết công thức tính thể tích của khối cầu là V=\(\dfrac{4}{3}\)πr3, với r là bán kính quả cầu.
Thể tích của quả cầu thép là: \(V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi.\left(0,15\right)^3=0,0045\pi\left(m^3\right)\)
Khối lượng của quả cầu thép là: \(m=DV=7850.0,0045\pi\approx111\left(kg\right)\)
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Đáp án D.
Khối nón cụt có thể tích là V = πh 3 R 2 + R . r + r 2 mà h = 3 V = π ⇒ R 2 + R . r + r 2 = 1 (*).
Ta có P = R + 2 r ⇔ R = P - 2 r thay vào (*), ta được P - 2 r 2 + P - 2 r r + r 2 = 1
⇔ P 2 - 4 P r + 4 r 2 + P r - 2 r 2 + r 2 - 1 = 0 ⇔ 3 r 2 - 3 P r + P 2 - 1 = 0 (I).
Vậy phương trình (I) có nghiệm khi và chỉ khi ∆ I = - 3 P 2 - 4 . 3 . P 2 - 1 ≥ 0 ⇔ P ≤ 2 .
Vậy giá trị lớn nhất của P là 2.
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h=3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P=R+2r
A. 2 3
B. 3.
C. 3 3
D. 2.
Mặt cầu bán kính r có diện tích bằng 36 π . Tìm thể tích V của khối cầu bán kính r.
A. V = 72 2 π
B. V = 288 π
C. V = 36 π
D. V = 18 π
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
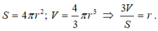
một quả cầu bằng thuỷ tinh có đường kính là 10cm; có khối lượng là 375g. Biết KLR của thuỷ tinh này là 2,5g/cm3 và thể tích của vật hình cầu được xác định theo công thức : V=4.3,14.R.R.R/3 ( với R là bán kính hình cầu)
a) Em có thể nói rằng quả cầu này là rỗng hay đặc được ko?Vì sao?
b) Nếu quả cầu này là rỗng thì hãy tính thể tích của phần rỗng đó
TK
Tóm tắt: R=5 cm
m=375 g
a, Thể tích của quả cầu là: V=4343.3,14.R³=4343.3,14.5³=1570315703 cm³
Khối lượng riêng của quả cầu là: D=m/V=375/1570315703≈0,72 g/cm³
⇒ Quả cầu rỗng
b, Nếu không rỗng thì thể tích thực của quả cầu là: Vt=m/D=375/2,5=150 cm³
thể tích phần rỗng là: Vr=V-Vt≈373,3333 cm³
( Bạn tự thay số vào công thức nha)
I. Trắc nghiệm ( 6 điểm)
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
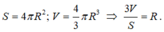
Một khối cầu có thể tích bằng 32 π 3 . Bán kính R của khối cầu đó là
A. R = 32
B. R = 2
C. R = 4
D. R = 2 2 3