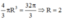Các câu hỏi tương tự
Mặt cầu bán kính r có diện tích bằng 36 π . Tìm thể tích V của khối cầu bán kính r.
A. V = 72 2 π
B. V = 288 π
C. V = 36 π
D. V = 18 π
Cho khối cầu có thể tích bằng
8
πa
3
6
27
, khi đó bán kính R của mặt cầu là A.
R
a
2
3
B.
R
a
6
2
C.
R...
Đọc tiếp
Cho khối cầu có thể tích bằng 8 πa 3 6 27 , khi đó bán kính R của mặt cầu là
A. R = a 2 3
B. R = a 6 2
C. R = a 3 3
D. R = a 6 3
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất. A.
h
2
R
3
3
.
B.
h
R
2...
Đọc tiếp
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
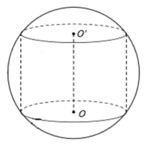
A. h = 2 R 3 3 .
B. h = R 2 2 .
C. h = R 3 3 .
D. h = R 2 .
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất A.
h
2
R
3
3
B.
h
R
2
2
C. ...
Đọc tiếp
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất
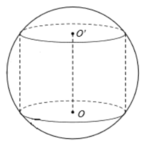
A. h = 2 R 3 3
B. h = R 2 2
C. h = R 3 3
D. h = R 2
Cho khối cầu (S) có tâm I, bán kính R không đổi. Một khối trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất. A.
R
2
B.
R
3
3
C. 4 D. 2
Đọc tiếp
Cho khối cầu (S) có tâm I, bán kính R không đổi. Một khối trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
A. R 2
B. R 3 3
C. 4
D. 2
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính đáy r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất. A.
h
R
2
B.
h
R
2
2
C.
h
R
3
3
D. ...
Đọc tiếp
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính đáy r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
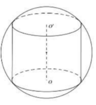
A. h = R 2
B. h = R 2 2
C. h = R 3 3
D. h = 2 R 3 3
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính r thay đổi, nối tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích khối nón lớn nhất A.
h
4
R
3
B.
h
R
C.
h
3
R
3
D.
h
R
2
Đọc tiếp
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính r thay đổi, nối tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích khối nón lớn nhất
A. h = 4 R 3
B. h = R
C. h = 3 R 3
D. h = R 2
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ có chiều cao h và bán kính r thay đổi nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích khối trụ lớn nhất. A.
h
R
2
B.
h
2
R
3
3
C.
h
R
3
3...
Đọc tiếp
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ có chiều cao h và bán kính r thay đổi nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích khối trụ lớn nhất.
A. h = R 2
B. h = 2 R 3 3
C. h = R 3 3
D. h = R 2 2
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính r thay đổi, nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích khối nón lớn nhất A.
h
R
2
B.
h
R
3
C.
h
4
R
3
D.
h
3...
Đọc tiếp
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính r thay đổi, nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích khối nón lớn nhất
A. h = R 2
B. h = R 3
C. h = 4 R 3
D. h = 3 R 2