Tìm giá trị lớn nhất của hàm số f x = e x + 1 - 2 trên đoạn [0;3].
![]()
![]()
![]()
![]()
\(f\left(x\right)=e^{sinx}-sinx-1\)
\(\Rightarrow f'\left(x\right)=cosx.e^{sinx}-cosx=cosx\left(e^{sinx}-1\right)\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\)
\(f\left(0\right)=0\) ; \(f\left(\dfrac{\pi}{2}\right)=e-2\) ; \(f\left(\pi\right)=0\)
\(\Rightarrow f\left(x\right)_{min}=0\) ; \(f\left(x\right)_{max}=e-2\)
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x) trên [ a; e]?
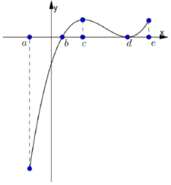
A. m a x [ a , e ] f ( x ) = f ( c ) m i n [ a , e ] f ( x ) = f ( a )
B. m a x [ a , e ] f ( x ) = f ( a ) m i n [ a , e ] f ( x ) = f ( b )
C. m a x [ a , e ] f ( x ) = f ( e ) m i n [ a , e ] f ( x ) = f ( b )
D. m a x [ a , e ] f ( x ) = f ( d ) m i n [ a , e ] f ( x ) = f ( b )
Ta có bảng biến thiên như hình vẽ sau:
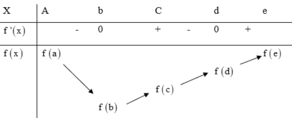
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
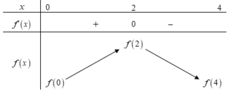
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
Cho hàm số f(x) = |2x − m|. Tìm m để giá trị lớn nhất của f(x) trên [1; 2] đạt giá trị nhỏ nhất.
A. m = −3
B. m = 2
C. m = 3
D. m = −2
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D
Cho hàm số f ( x ) = sin x - m sin x + 1 . Tìm giá trị của tham số m để giá trị lớn nhất của hàm số trên đoạn 0 ; 2 π 3 bằng -2?
A. m = 5
B. m = 5 m = 2
C. m = 2
D. m = 3
Cho hàm số \(y=f\left(x\right)=x^2+2\left(m-1\right)x+3m-5\) (m là tham số). Tìm m để giá trị nhỏ nhất của f(x) đạt giá trị lớn nhất
Dễ thấy: \(f\left(x\right)=\left(x+m-1\right)^2-m^2+5m-6\ge-m^2+5m-6\)
Giá trị nhỏ nhất của f(x) đạt lớn nhất tức \(-m^2+5m-6\) đạt lớn nhất
Mà \(g\left(m\right)=-m^2+5m-6=-\left(m-\dfrac{5}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
g(m) đạt lớn nhất khi m=5/2
m cần tìm là 5/2
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(f\left(x\right)=\sqrt{x+1}+\sqrt{3-x}\)
ĐKXĐ : \(-1\le x\le3\)
- ADbu nhi : \(\left(\sqrt{x+1}+\sqrt{3-x}\right)^2\le\left(1^2+1^2\right)\left(\left(\sqrt{x+1}\right)^2+\left(\sqrt{3-x}\right)^2\right)\)
\(=2\left(x+1+3-x\right)=2.4=8\)
\(\Rightarrow\sqrt{x+1}+\sqrt{3-x}\le\sqrt{8}=2\sqrt{2}\)
- Dấu " = " xảy ra \(\Leftrightarrow\dfrac{1}{\sqrt{x+1}}=\dfrac{1}{\sqrt{3-x}}\)
\(\Leftrightarrow x+1=3-x\)
\(\Leftrightarrow x=1\left(TM\right)\)
\(\Rightarrow Max_{f\left(x\right)}=2\sqrt{2}\) tại x = 1.
- Có : \(\sqrt{x+1}+\sqrt{3-x}\ge\sqrt{x+1+3-x}=\sqrt{4}=2\)
- Dấu " = " xảy ra <=> x = -1 ( TM )
\(\Rightarrow Min_{f\left(x\right)}=2\) tại x = - 1 .
Cho hàm số y = f(x) xác định và liên tục trên [-2;2], có đồ thị của hàm số y= f'(x) như sau: Tìm giá trị x 0 để hàm số y=f(x) đạt giá trị lớn nhất trên [-2;2].
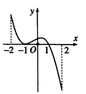
A. x 0 = 2
B. x 0 = -1
C. x 0 = -2
D. x 0 = 1