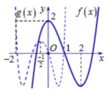
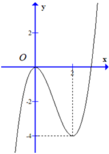
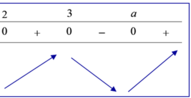
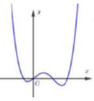
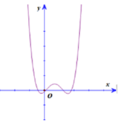
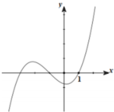
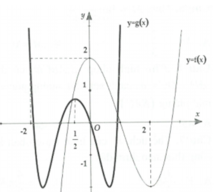
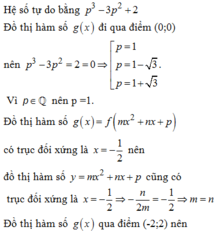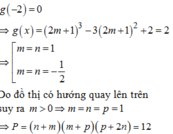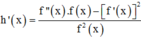Cho hàm số bậc ba f(x) và g x = f mx 2 + nx + p m , n , p ∈ ℚ có đồ thị như hình dưới (đường nét đậm là đồ thị của hàm g(x) đường thẳng x = - 1 2 là trục đối xứng của đồ thị hàm số g x Giá trị của biểu thức
P = ( n+m)(m+p)(p+2n) bằng bao nhiêu?
A. 12
B. 16
C. 24
D. 6