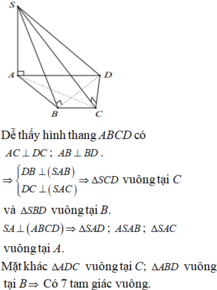
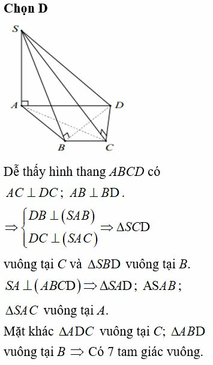
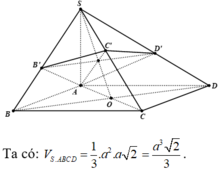
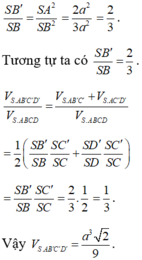Cho hình chóp S . A B C D có đáy ABCD là hình thang, A D / / B C , A D = 3 B C . M , N lần lượt là trung điểm AB, CD. G là trọng tâm Δ S A D . Mặt phẳng G M N cắt hình chóp S . A B C D theo thiết diện là:
A. Hình bình hành
B. Δ G M N
C. Δ S M N
D. Ngũ giác