Cho MN //PQ và MQ//NP. Tính x.
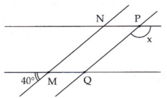
A. 100 ° ;
B. 140 ° ;
C. 180 ° ;
D. Kết quả khác
Bài 1: Cho hình thang MNPQ có đáy MN//PQ
a) Cho biết MQ//NP. Chứng minh rằng MN=PQ; MQ=NP
b) Cho biết MN=PQ. Chứng minh rằng MQ//NP; MQ=NP
Bài 2: Cho tứ giác MNPQ có MN=MQ; PN=PQ; góc M=50 độ; góc P=90 độ
a) Tính số đo góc MQN b) Tính số đo góc MQP
c) Chứng minh MP vuông góc với NQ
Các bạn giúp mình nhé. Cảm ơn các bạn.
Bài 1: Cho hình thang MNPQ có đáy MN//PQ
a) Cho biết MQ//NP. Chứng minh rằng MN=PQ; MQ=NP
b) Cho biết MN=PQ. Chứng minh rằng MQ//NP; MQ=NP
Bài 2: Cho tứ giác MNPQ có MN=MQ; PN=PQ; góc M=50 độ; góc P=90 độ
a) Tính số đo góc MQN b) Tính số đo góc MQP
c) Chứng minh MP vuông góc với NQ
Các bạn giúp mình nhé. Cảm ơn các bạn.
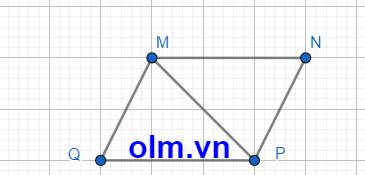
Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
\(\widehat{QPM}\) = \(\widehat{PMN}\) (2 góc so le trong)
\(\widehat{QMP}\) = \(\widehat{NPM}\) (2 góc so le trong)
\(\Rightarrow\) \(\Delta\)MPQ = \(\Delta\)PMN (g-c-g)
\(\Rightarrow\) PQ = MN; MQ = PN (đpcm)
b, Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
MN = PQ
\(\widehat{QPM}\) = \(\widehat{PMN}\) ( 2 góc so le trong)
⇒\(\Delta\)MPQ = \(\Delta\)PMN ( cạnh góc cạnh)
\(\Rightarrow\) MQ = NP (đpcm)
⇒ \(\widehat{QMP}\) = \(\widehat{NPM}\)
Mà hai góc \(\widehat{QMP}\) và \(\widehat{NPM}\) ở vị trí so le trong và bằng nhau nên:
QM // NP (đpcm)
Bài 1: Cho hình thang MNPQ có đáy MN//PQ
a) Cho biết MQ//NP. Chứng minh rằng MN=PQ; MQ=NP
b) Cho biết MN=PQ. Chứng minh rằng MQ//NP; MQ=NP
Bài 2: Cho tứ giác MNPQ có MN=MQ; PN=PQ; góc M=50 độ; góc P=90 độ
a) Tính số đo góc MQN b) Tính số đo góc MQP
c) Chứng minh MP vuông góc với NQ
Các bạn giúp mình nhé. Cảm ơn các bạn.
bài 1 :
a) Ta có MQ//NP (theo giả thiết).
Chứng minh MN = PQ:
Vì MN//PQ và MQ//NP, ta có hai tam giác MNP và QMQ' đồng dạng (theo nguyên lý đồng dạng của tam giác có hai cặp góc tương đồng bằng nhau).
Do đó, ta có tỉ số đồng dạng giữa các cạnh của hai tam giác là:
MN/MQ = NP/QM
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MN/MQ = NP/NP
Từ đó suy ra: MN = PQ.
Chứng minh MQ = NP:
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MQ/MN = NP/PQ
Vì MN = PQ (đã chứng minh ở trên), nên ta có tỉ số đồng dạng:
MQ/MN = NP/NP
Từ đó suy ra: MQ = NP.
b) Ta có MN = PQ (theo giả thiết).
Chứng minh MQ//NP:
Giả sử MQ không // NP. Khi đó, MQ và NP sẽ cắt nhau tại một điểm O.
Vì MN//PQ và MQ//NP, nên ta có hai tam giác MNP và QMQ' đồng dạng (theo nguyên lý đồng dạng của tam giác có hai cặp góc tương đồng bằng nhau).
Do đó, ta có tỉ số đồng dạng giữa các cạnh của hai tam giác là:
MN/MQ = NP/QM
Từ đó suy ra: MN/MQ = NP/NP
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MN/MQ = NP/NP
Từ đó suy ra: MN = PQ.
Điều này mâu thuẫn với giả thiết MN = PQ (đã cho). Vậy giả sử MQ không // NP là sai.
Do đó, ta kết luận rằng MQ//NP.
Chứng minh MQ = NP:
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MQ/MN = NP/PQ
Vì MN = PQ (đã chứng minh ở trên), nên ta có tỉ số đồng dạng:
MQ/MN = NP/NP
Từ đó suy ra: MQ = NP.
bài 2 :
a) Ta có MN = MQ và góc M = 50 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc N = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
50 độ + góc N + 90 độ + góc N = 360 độ
Simplifying the equation:
140 độ + 2góc N = 360 độ
Trừ 140 độ từ hai phía:
2góc N = 220 độ
Chia cho 2:
góc N = 110 độ
Vậy số đo góc MQN là 110 độ.
b) Ta đã biết góc P = 90 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc M = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
góc M + 110 độ + 90 độ + góc M = 360 độ
Simplifying the equation:
2góc M + 200 độ = 360 độ
Trừ 200 độ từ hai phía:
2góc M = 160 độ
Chia cho 2:
góc M = 80 độ
Vậy số đo góc MQP là 80 độ.
c) Để chứng minh MP vuông góc với NQ, ta cần chứng minh rằng góc MPN + góc NQP = 90 độ.
Ta đã biết góc P = 90 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc M = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
góc M + góc N + 90 độ + góc M = 360 độ
Simplifying the equation:
2góc M + góc N = 270 độ
Vì góc M = góc Q, nên ta có:
2góc M + góc M = 270 độ
Bài 1: Cho hình thang MNPQ có đáy MN//PQ
a) Cho biết MQ//NP. Chứng minh rằng MN=PQ; MQ=NP
b) Cho biết MN=PQ. Chứng minh rằng MQ//NP; MQ=NP
Bài 2: Cho tứ giác MNPQ có MN=MQ; PN=PQ; góc M=50 độ; góc P=90 độ
a) Tính số đo góc MQN b) Tính số đo góc MQP
c) Chứng minh MP vuông góc với NQ
Các bạn giúp mình nhé. Cảm ơn các bạn.
Bài 7: Cho hình vẽ bên Biết MN//PQ, MN = PQ. Chứng minh MQ = NP và MQ //NP.
MN//PQ, MN = PQ⇒MNPQ là hình bình hành⇒MQ=NP, MQ //NP.
Xét tứ giác MNPQ có
MN//PQ
MN=PQ
Do đó: MNPQ là hình bình hành
=>MQ//NP và MQ=NP
MN//PQ, MN = PQ⇒MNPQ là hình bình hành⇒MQ=NP, MQ //N
cho tứ giác MNPQ có MN=PQ,MQ=NP chứng minh:
a) tam giác MNP=tam giác PQM
b) MN//PQ và MQ//NP
a: Xét ΔMNP và ΔPQM có
MN=PQ
NP=QM
MP chung
=>ΔMNP=ΔPQM
b: Xét tứ giác MNPQ có
MQ=NP
MN=PQ
=>MNPQ là hình bình hành
=>MN//PQ và MQ//NP
3) Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.a) Chứng minh: AMNC là hình thang, tính AC, biết MN = 3cm.b) Chứng minh: PQ ∥AC.c) Chứng minh: MN ∥PQ và MN = PQ.d) MQ = NP và MQ ∥NP.
Cho hình bs.9. Khi đó
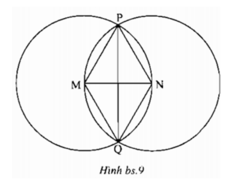
(A) MP = MQ = MN = PQ;
(B) MP = MQ = NQ = NP;
(C) MP = MQ = NP = PQ;
(D) MP = MQ > NQ = NP;
Cho 2 đoạn thẳng MN và PQ cắt nhau tại O. Nối M với P ,N với Q
a, Tính tổng các góc MPN,MQN,PMQ,PNQ\
b, So sánh MN+PQ voi MQ+NP,MP+NQ
MN+PQvoi MP+NQ+MQ+NP