MN//PQ, MN = PQ⇒MNPQ là hình bình hành⇒MQ=NP, MQ //NP.
Xét tứ giác MNPQ có
MN//PQ
MN=PQ
Do đó: MNPQ là hình bình hành
=>MQ//NP và MQ=NP
MN//PQ, MN = PQ⇒MNPQ là hình bình hành⇒MQ=NP, MQ //N
MN//PQ, MN = PQ⇒MNPQ là hình bình hành⇒MQ=NP, MQ //NP.
Xét tứ giác MNPQ có
MN//PQ
MN=PQ
Do đó: MNPQ là hình bình hành
=>MQ//NP và MQ=NP
MN//PQ, MN = PQ⇒MNPQ là hình bình hành⇒MQ=NP, MQ //N
Cho hình vẽ bên. Chứng minh rằng:
a) MNQ =PQN;
b) MN song song với PQ ;
c) MQ song song với NP ; 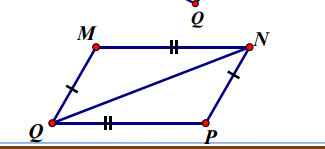
cho tứ giác MNPQ có MN=PQ,MQ=NP chứng minh:
a) tam giác MNP=tam giác PQM
b) MN//PQ và MQ//NP
Cho 2 đoạn thẳng MN và PQ cắt nhau tại O. Nối M với P ,N với Q
a, Tính tổng các góc MPN,MQN,PMQ,PNQ\
b, So sánh MN+PQ voi MQ+NP,MP+NQ
MN+PQvoi MP+NQ+MQ+NP
Cho MN //PQ và MQ//NP. Tính x.
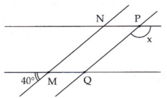
A. 100 ° ;
B. 140 ° ;
C. 180 ° ;
D. Kết quả khác
Cho tam giác MNP vuông tại M (MP < MN). Trên cạnh MN lấy điểm Q sao cho MQ = MP, trên tia đối của tia MP lấy điểm R sao cho MR = MN. Chứng minh:
a) P Q ⊥ N R .
b) R Q ⊥ N P .
Cho hai đoạn thẳng MN và PQ cắt nhau tại trung điểm O của mỗi đoạn a) chứng minh tam giác MOQ= tam giác NOP b) Lấy D thuộc đoạn MQ và E thuộc đoạn NP sao cho MD=NE.Chứng minh O là trung điểm của DE
Cho tam giác MNP. Tại đỉnh M dựng góc xMN so le trong với góc N. Trên tia Mx lấy điểm Q sao cho đoạn thẳng MQ=NP, đoạn thẳng PQ cắt đoạn thẳng MN tại O.
a) chứng minh O là trung điểm đoạn thẳng MN.
b) chứng minh 2 tam giác MOP và NOQ bằng nhau.
Cho tam giác MNP( MN<MP) có MQ là phân giác của góc M( Q thuộc NP). Trên MP lấy điểm E sao cho ME=MN
a) Chứng minh: NQ= QE
b) Gọi H là giao điểm của MN và EQ. Chứng minh: Tam giác EMH bằng tam giâc NMP. Từ đó, suy ra tam giác MHP là tam giác cân
c) Hãy so sánh NQ và PQ
Cho tam giác MNP (MN<MP) có MQ là phân giác của \(\widehat{M}\)\(\left(Q\in NP\right)\). Trên MP lấy điểm E sao cho ME=MN
a) Chứng minh NQ=QE
b) Gọi H là giao điểm của MN và EQ. Chứng minh \(\Delta EMH=\Delta NMP\)
c) So sánh NQ và PQ