Trong các hình dưới đây, hình nào là hình bình hành:
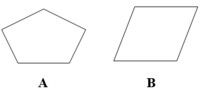
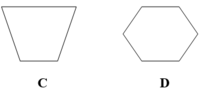
A. Hình A
B. Hình B
C. Hình C
D. Hình D
Những câu hỏi liên quan
Hình bình hành có đáy là 6dm,chiều cao là 4dm.diện tích hình hình bình hành đó là:
A:20dm2
B:10dm
C:24dm2
D:24dm
16 tháng 11 2021 lúc 14:10
Trong hình bình hành ABCD có số đo góc A gấp 2 lần góc B . Số đo các góc của hình bình hành là :
Vì ABCD là hbh nên AD//BC \(\Rightarrow\widehat{A}+\widehat{B}=180^0\Rightarrow3\widehat{B}=180^0\Rightarrow\widehat{B}=60^0\Rightarrow\widehat{A}=120^0\)
Vì ABCD là hbh nên \(\left\{{}\begin{matrix}\widehat{B}=\widehat{D}=60^0\\\widehat{A}=\widehat{C}=120^0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
16 tháng 11 2021 lúc 14:12
Trong hình bình hành ABCD có số đo góc A gấp 2 lần góc B . Số đo các góc của hình bình hành là :
Vì ABCD là hình bình hành nên ˆA=ˆCA^=C^ và ˆB=ˆDB^=D^ (tính chất)
Áp dụng định lý tổng các góc trong một tứ giác ta có:
Đúng 0
Bình luận (0)
1. Cho hình bình hành ABCD có AB 2AD. Gọi M, N theo tứ tự là trung điểm của các cạnh AB, CD. Gọi P và Q lần lượt là giao điểm của BN với CM và của AN với DMa. Tứ giác AMND là hình gì? Vì sao?b. Chứng minh: tứ giác MPNQ là hình chữ nhậtc. Tìm điều kiện của tứ giác ABCD để MPNQ là hình vuôngd. Chứng minh: bốn đường thẳng AC, BD, MN, QP đồng qui2. Cho hình bình hành ABCD. Kẻ AN, CM vuông góc với BD, N và M thuộc BDa. Chứng minh DN BM b. Ch...
Đọc tiếp
1. Cho hình bình hành ABCD có AB= 2AD. Gọi M, N theo tứ tự là trung điểm của các cạnh AB, CD. Gọi P và Q lần lượt là giao điểm của BN với CM và của AN với DM
a. Tứ giác AMND là hình gì? Vì sao?
b. Chứng minh: tứ giác MPNQ là hình chữ nhật
c. Tìm điều kiện của tứ giác ABCD để MPNQ là hình vuông
d. Chứng minh: bốn đường thẳng AC, BD, MN, QP đồng qui
2. Cho hình bình hành ABCD. Kẻ AN, CM vuông góc với BD, N và M thuộc BD
a. Chứng minh DN = BM
b. Chứng minh Tứ giác ANCM là hình bình hành
c. Gọi K là điểm đối xứng với A qua N. Tứ giác DKCB là hình gì? Vì sao?
d. Tia AM cắt tia KC tại P. Chứng minh các đường thẳng AC, PN, KM đồng qui
Cho hình bình hành ABCD. Vẽ ở ngoài hình bình hành các hình vuông có cạnh theo thứ tự là AB,BC,CD,DA có tâm đối xứng là E,F,G,H.Chứng minh rằng:
a/Tam giác HAE= tam giác FBE
b/EFGH là hình vuông
Bài 1: Tam giác ABC có AM, BN là các trung tuyến, G là trọng tâm. Gọi E và F lầnlượt là trung điểm của GB và GA. Gọi I là điểm đối xứng với G qua M.a) Chứng minh BICG và MNFE là hình bình hành.b) Để MNFE là hình chữ nhật thì cần có thêm điều kiện gì cho tam giác ABC ?c) Khi BICG là hình thoi, hãy chứng minh tam giác ABC cân tại A.Bài 2: Cho hình bình hành ABCD. Gọi E là điểm đối xứng của A qua trung điểm Mcủa BC.a) Chứng minh ABEC là hi...
Đọc tiếp
Bài 1: Tam giác ABC có AM, BN là các trung tuyến, G là trọng tâm. Gọi E và F lần
lượt là trung điểm của GB và GA. Gọi I là điểm đối xứng với G qua M.
a) Chứng minh BICG và MNFE là hình bình hành.
b) Để MNFE là hình chữ nhật thì cần có thêm điều kiện gì cho tam giác ABC ?
c) Khi BICG là hình thoi, hãy chứng minh tam giác ABC cân tại A.
Bài 2: Cho hình bình hành ABCD. Gọi E là điểm đối xứng của A qua trung điểm M
của BC.
a) Chứng minh ABEC là hình bình hành và D, E, C thẳng hàng.
b) Tam giác ABC phải có điều kiện gì thì ABEC trở thành hình thoi.
a, xét tứ giác BICG có :
M là trung điểm cuả BC do AM là trung tuyến (gt)
M là trung điểm của GI do I đx G qua M (gt)
=> BICG là hình bình hành (dh)
+ G là trọng tâm của tam giác ABC (gt)
=> GM = AG/2 và GN = BG/2 (đl)
E; F lần lượt là trung điểm của GB; GA (gt) => FG = AG/2 và GE = BG/2 (tc)
=> FG = GM và GN = GE
=> G là trung điểm của FM và EN
=> MNFE là hình bình hành (dh)
b, MNFE là hình bình hành (câu a)
để MNFE là hình chữ nhật
<=> NE = FM
có : NE = 2/3BN và FM = 2/3AM
<=> AM = BN mà AM và BN là trung tuyến của tam giác ABC (Gt)
<=> tam giác ABC cân tại C (đl)
c, khi BICG là hình thoi
=> BG = CG
BG và AG là trung tuyến => CG là trung tuyến
=> tam giác ABC cân tại A
Cho ΔABC vuông cân tại A. Gọi D;E;F lần lược là trung điểm của AB;BC;AC
a, C/m tứ giác ADEF là hình vuông
b, Gọi I là điểm đối xứng của E qua D. C/m tứ giác ACEI là hình bình hành
c, Tứ giác ACBI là hình gì ?
M.n vẽ hình giúp em nữa ạ Thank nhiều
a: Xét ΔABC có
E là trung điểm của BC
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔABC
Suy ra: EF//AD và EF=AD
Xét tứ giác ADEF có
EF//AD
EF=AD
Do đó: ADEF là hình bình hành
mà \(\widehat{FAD}=90^0\)
nên ADEF là hình chữ nhật
mà AD=AF
nên ADEF là hình vuông
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SASC, SBSD. Trong các khẳng định sau, khẳng định nào đúng ? A.
S
A
⊥
A
B
C
D
B.
S
O
⊥
A
B
C
D
C.
S
C
⊥...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA=SC, SB=SD. Trong các khẳng định sau, khẳng định nào đúng ?
A. S A ⊥ A B C D
B. S O ⊥ A B C D
C. S C ⊥ A B C D
D. S B ⊥ A B C D
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SASC, SBSD. Trong các khẳng định sau, khẳng định nào đúng ? A.
S
A
⊥
(
A
B
C
D
)
B.
S
O
⊥
(
A
B
C
D...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA=SC, SB=SD. Trong các khẳng định sau, khẳng định nào đúng ?
A. S A ⊥ ( A B C D )
B. S O ⊥ ( A B C D )
C. S C ⊥ ( A B C D )
D. S B ⊥ ( A B C D )
