Trong mặt phẳng Oxy cho parabol ( P ) : y = 1 4 x 2 và đường thẳng d : y = x + 3.
1) Vẽ (P) và d trên cùng một hệ trục tọa độ.
2) Tìm tọa độ giao điểm của (P) và d.
Trong mặt phẳng toạ độ Oxy, cho parabol (P) y=x^2 và đường thẳng (d) y=x+2.
a) vẽ parabol (P) và đường thẳng (d) trên cùng mặt phẳng toạ độ Oxy.
b) Tìm toạ độ giao điểm của (P) và (d) bằng phép tính.
c) viết phương trình đường thẳng (d') có dạng y=ax+b , biết (d') song song với (d) và đi qua điểm M(2:5)
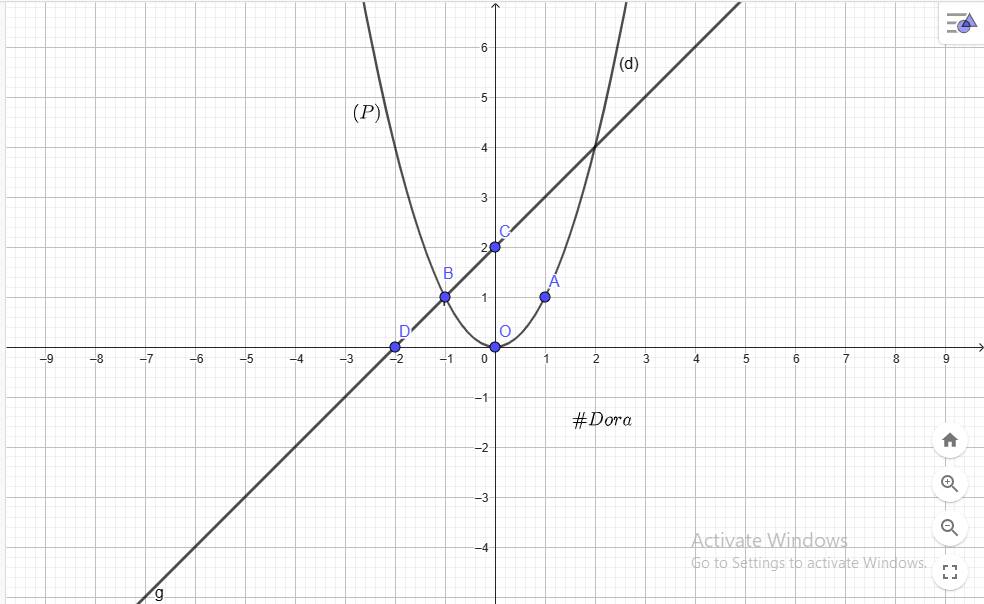
`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`
Trong mặt phẳng tọa độ Oxy, cho parabol (P): y=x2 và đường thẳng (d): y=2(m-1)x+5-2m (m là tham số)
a) Vẽ đồ thị parabol (P).
b) Biết đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt. Gọi hoành độ giao điểm của đường thẳng (d) và parabol (P) là x1, x2. Tìm m để x+x=6
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=2\left(m-1\right)x+5-2m\)
\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
Ta có: \(x_1+x_2=6\)
\(\Leftrightarrow2\left(m-1\right)=6\)
\(\Leftrightarrow m-1=3\)
hay m=4
Vậy: m=4
Trong mặt phẳng tọa độ Oxy, cho đường thắng d: y= 2(m + 1)x – 2m và parabol P: y = x^2. Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm có hoành độ x1,x2 sao cho √x1 + √x2= √2
2. Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=X’ và đường thẳng (d):
y=3x+m² -1
a) Tìm m để đường thẳng (d) đi qua điểm A(-1: 5).
b) Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ x,,, thỏa
mãn |x|+2|x|=3.
Trong mặt phẳng Oxy, cho parabol (P): y=xả và đường thẳng (d): y=2(m+1)x-m2 – 2
a) Tìm m để (d) cắt (P) tại hai điểm A và B phân biệt.
Phương trình giao điểm:
`x^2=2(m+1)x-m^2-2`
`<=>x^2-2(m+1)+m^2+2=0` (1)
(d) cắt (P) tại 2 điểm phân biệt `<=>` PT (1) có 2 nghiệm phân biệt.
`<=> \Delta' >0`
`<=> (m+1)^2-(m^2+2)>0`
`<=>2m-1>0`
`<=>m>1/2`
Trong mặt phẳng tọa độ Oxy, cho Parabol(P): y=x2 và đường thẳng (d): y=2(m+1)x-m2-4 (1), (m là tham số)
a) Tìm m để đường thẳng (d) đi qua A(0;-5)
b) Với giá trị nào của m để đường thẳng (d) cắt parabol (P) tại 2 điểm phân biệt có hoành độ x1; x2 thỏa mãn điều kiện: (2x1-1)(x22-2mx2+m2+3)=21
a: Thay x=0 và y=-5 vào (d), ta được:
2(m+1)*0-m^2-4=-5
=>m^2+4=5
=>m=1 hoặc m=-1
b:
PTHĐGĐ là;
x^2-2(m+1)x+m^2+4=0
Δ=(2m+2)^2-4(m^2+4)
=4m^2+8m+4-4m^2-16=8m-12
Để PT có hai nghiệm phân biệt thì 8m-12>0
=>m>3/2
x1+x2=2m+2; x1x2=m^2+4
(2x1-1)(x2^2-2m*x2+m^2+3)=21
=>(2x1-1)[x2^2-x2(2m+2-2)+m^2+4-1]=21
=>(2x1-1)[x2^2+2x2-x2(x1+x2)+x1x2-1]=21
=>(2x1-1)(x2^2+2x2-x1x2-x2^2+x1x2-1]=21
=>(2x1-1)(2x2-1)=21
=>4x1x2-2(x1+x2)+1=21
=>4(m^2+4)-2(2m+2)+1=21
=>4m^2+16-4m-4-20=0
=>4m^2-4m-8=0
=>(m-2)(m+1)=0
=>m=2(nhận) hoặc m=-1(loại)
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình và đường thẳng (d) có phương trình
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình
và đường thẳng (d) có phương trình
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định
a:
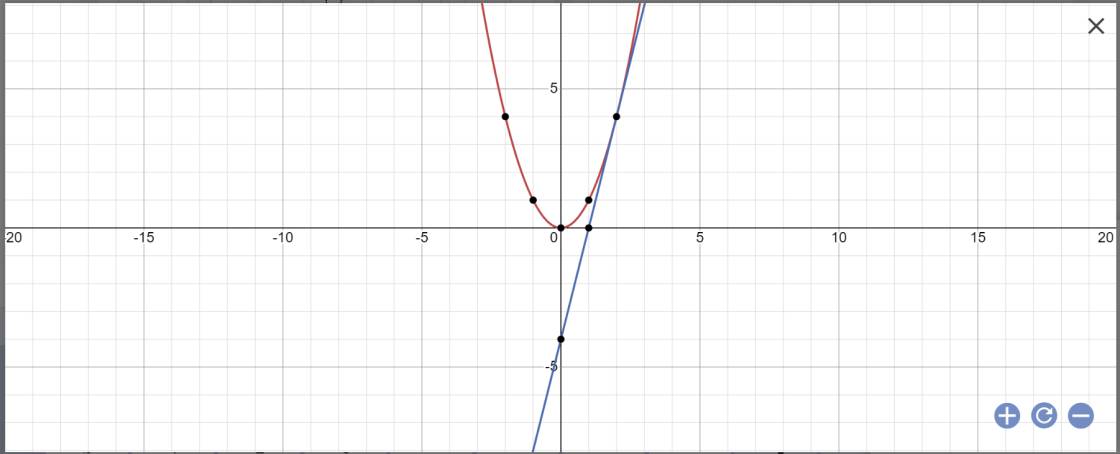
b: PTHĐGĐ là:
2x^2-(2m-2)x+m-1=0
Δ=(2m-2)^2-4*2*(m-1)
=4m^2-8m+4-8m+8
=4m^2-16m+12
=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)
Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0
=>m>3 hoặc m<1
trong mặt phẳng Oxy, cho parabol (P) y =ax2 a khác 0 và đường thẳng d : y = x-1
a) tìm a biết P tiếp xúc d
ta có pt hoảnh độ giao điểm: \(ax^2=x-1\Leftrightarrow ax^2-x+1=0\)
P tiếp xúc d <=> PT trên có nghiệm kép <=> \(\Delta=0\Leftrightarrow1-4a=0\Leftrightarrow a=\frac{1}{4}\)
Trong mặt phẳng tọa độ Oxy, cho parabol: \(\left(P\right):y=x^2\) và đường thẳng (d): y=\(3x+m^2-1\). Xác định m để (d) và (P) cùng đi qua điểm có tung độ bằng 1
Thay y=1 vào (P), ta được:
\(x^2=1\)
=>x=1 hoặc x=-1
Thay x=1 và y=1 vào (d), ta được:
\(m^2-1+3=1\)(vô lý)
Thay x=-1 và y=1 vào (d), ta được:
\(m^2-1-3=1\)
\(\Leftrightarrow m^2=5\)
hay \(m\in\left\{\sqrt{5};-\sqrt{5}\right\}\)
tham khảo
Thay y=1 vào (P), ta được:
\(x^2=1\)
=>x=1 hoặc x=-1
Thay x=1 và y=1 vào (d), ta được:
\(m^2-1+3=1\)(vô lý)
Thay x=-1 và y=1 vào (d), ta được:
\(m^2-1-3=1\)
\(\Leftrightarrow m^2=5\)
hay \(m\in\left\{\sqrt{5};-\sqrt{5}\right\}\)
Trong mặt phẳng tọa độ Oxy cho parabol (p) có pt y=1/2x^2 và đường thẳng d có pt y=-mx+3-m(vs m tham số) a)tìm tọa độ điểm M € parabol biết M có hoành độ =4
Thay x=4 vào (P), ta được:
y=1/2*4^2=8