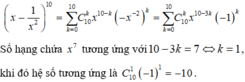(x^2+1/x)^4

\(=C^0_4\cdot\left(x^2\right)^4+C^1_4\cdot\left(x^2\right)^3\cdot\left(\dfrac{1}{x}\right)+C^2_4\cdot\left(x^2\right)^2\cdot\left(\dfrac{1}{x}\right)^2+C^3_4\cdot\left(x^2\right)^1\cdot\left(\dfrac{1}{x}\right)^3+C^4_4\cdot\left(x^2\right)^0\cdot\left(\dfrac{1}{x}\right)^4\)

=x^8+4x^5+6x^3+4/x+1/x^4

Ta có:

\({(2 + 3x)^4} = C_4^0{2^4} + C_4^1{2^3}3x + C_4^2{2^2}{\left( {3x} \right)^2} + C_4^32.{\left( {3x} \right)^3} + C_4^4{\left( {3x} \right)^4}\)

=> Hệ số của của \({x^2}\)là \(C_4^2{.2^2}{.3^2} = 36C_4^2.\)

Chọn D.

SHTQ của \(\left(3x+2\right)^5\) là \(C^k_5\cdot\left(3x\right)^{5-k}\cdot2^k=C^k_5\cdot3^{5-k}\cdot2^k\cdot x^{5-k}\)

Hệ số của số hạng chứa x tương ứng với 5-k=1

=>k=4

=>Hệ số là \(C^4_5\cdot3^{5-4}\cdot2^4=240\)

Ta có:

\({(2x + 3)^5} = 32{x^5} + 240{x^4} + 720{x^3} + 1080{x^2} + 810x + 243\)

Hệ số của \({x^3}\) là 720

Hệ số của \({x^4}\) là 240.  

Vậy  hệ số của \({x^3}\) lớn hơn hệ số của \({x^4}\).

SHTQ là: \(C^k_4\cdot\left(x^3\right)^{4-k}\cdot\left(\dfrac{1}{x}\right)^k=C^k_4\cdot x^{12-4k}\)

Số hạng ko chứa x tương ứng với 12-4k=0

=>k=3

=>SH đó là \(C^3_4=4\)

xy⁵  -5xy⁴+10xy³-10xy²+5xy-1

Đáp án C

Ta có P ( x ) = 1 + 2 x 12 = ∑ k = 0 12 C 12 k 1 12 - k = ∑ k = 0 12 C 12 k 2 k x k .

Gọi a k = C 12 K 2 K , 0 ≤ k ≤ 12 , k ∈ ℕ  là hệ số lớn nhất trong khai triển.

Suy ra a k ≥ a k + 1 a k ≥ a k - 1 ⇔ c 12 k 2 k ≥ c 12 k + 1 2 k + 1 c 12 k 2 k ≥ c 12 k - 1 2 k - 1  

⇔ 12 ! 12 - k ! k ! . 2 k ≥ 12 ! 11 - k ! k + 1 ! . 2 k + 1 12 ! 12 - k ! k ! . 2 k ≥ 12 ! 13 - k ! k + 1 ! . 2 k - 1 ⇔ 1 12 - k ≥ 2 k + 1 1 k ≥ 1 2 13 - k

Vậy hệ số lớn nhất trong khai triển đã cho là a 8 = 2 8 c 12 8 = 126720 .

Đáp án C

Ta có khai triển nhị thức Newton