Một chiếc cổng hình parabol dạng y = - x 2 / 2 có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (h.25).
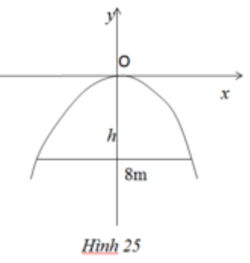
Một chiếc cổng parabol có phương trình y = (1/2)x^2. Biết cổng rộng d = 5m. Tính chiều cao của cổng
Mặt cắt cổng vào một khu triển lãm có hình dạng một parabol (P): y = -x^2. Mà trục đối xứng OH vuông góc với mặt đất. Biết bề rộng AB của cổng là 4m. Tính chiều cao HO của cổng.
Do tính đối xứng của parabol, \(\Rightarrow H\) là trung điểm AB \(\Rightarrow y_H=y_A=y_B\) đồng thời \(x_A=-x_B\)
Mặt khác \(AB=\left|x_A-x_B\right|=\left|2x_A\right|=4\Rightarrow x_A=2\)
\(\Rightarrow y_A=-x_A^2=-4\Rightarrow y_H=-4\)
\(\Rightarrow OH=\left|y_H\right|=4\) (m)
Một chiếc cổng có hình dạng một phần parabol với chiều
rộng BC d = = 8m(tham khảo hình vẽ). Một người cao 1,65m đứng
thẳng cách chân cổng C một khoảng 45cm thì đỉnh đầu vừa chạm
cổng. Tính gần đúng chiều cao h của cổng.
Một chiếc cổng hình parabl dạng \(y=-\dfrac{1}{2}x^2\) có chiều rộng \(d=8m\). Hãy tính chiều cao h của cổng (h.25) ?
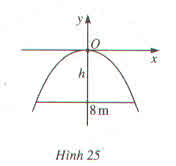
Lời giải
Parabol nhận trục tung là trục đối xứng
(điểm thấp nhất thuộc đồ thị có tọa độ A(4,ya)
\(y\left(4\right)=-\dfrac{1}{2}.4^2=-8\)
Vậy chiều cao cổng là 8m
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽbên). Tỉ số A B C D bằng :

A. 1 2
B. 4 5
C. 1 2 3
D. 3 1 + 2 2
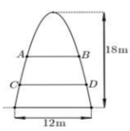
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽbên). Tỉ số A B C D bằng :
A. 1 2
B. 4 5
C. 1 2 3
D. 3 1 + 2 2
Đáp án C
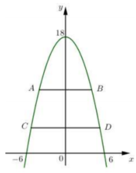


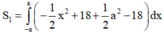



Diện tích hình phẳng giới hạn bởi parabol và đường thẳng CD là:

= − c 3 6 + c 3 2 − c 3 6 − c 3 2 = 2 c 3 3 S 1 = 2 3 S ⇒ 2 3 c 3 = 2 3 .144 = 96 ⇒ c = 2 18 3 ⇒ C D = 2 c ⇒ 4 18 3 ⇒ A B C D = 1 2 3
Một cổng chào có dạng hình Parabol chiều cao18m, chiều rộng chân đế12m. Người ta căng hai sợi dây trang trí AB, CDnằm ngang đồng thời chia hình giới hạn bởi Parabol và mặt đất thành ba phần có diện tích bằng nhau . Tỉ số AB/CD bằng
A. 3 1 + 2 2
B. 1 2
C. 4/5.
D. 1 2 3
Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m.
Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
Gọi phương trình của parabol là \({y^2} = 2px\)
Ta có chiều cao của cổng \(OH = BK = 10\), chiều rộng tại chân cổng \(BD = 2BH = 5\)
Vậy điểm B có tọa độ là \(B\left( {10;\frac{5}{2}} \right)\)
Thay tọa độ điểm B vào phương trình parabol ta có:
\({\left( {\frac{5}{2}} \right)^2} = 2p.10 \Rightarrow p = \frac{5}{{16}}\), suy ra phương trình parabol có dạng \({y^2} = \frac{5}{8}x\)
Thay \(x = 2\) vào phương trình \({y^2} = \frac{5}{8}x\) ta tìm được \(y = \frac{{\sqrt 5 }}{2}\)
Vậy bề rộng của cổng tại chỗ cách đỉnh 2 m là \(\sqrt 5 \) m