Chu kì của hàm số y = sinx/3 là
A. 2π
B. 6π
C. π/3
D. 2π/3
Những câu hỏi liên quan
Hàm số y = sinx đồng biến trên đoạn nào dưới đây ?
A . [ π ; 2π ]
B . [-π ; π ]
C . [ 0 ; π ]
D . [ 0 ; \(\dfrac{\pi}{2}\)]
????????????????????
Cho các mệnh đề sau(I) Hàm số
f
x
sin
x
x
2
+
1
là hàm số chẵn.(II) Hàm số
f
x
3
sin
x
+
4
cos
x
có giá trị lớn nhất là 5.(III) Hàm số
f...
Đọc tiếp
Cho các mệnh đề sau
(I) Hàm số f x = sin x x 2 + 1 là hàm số chẵn.
(II) Hàm số f x = 3 sin x + 4 cos x có giá trị lớn nhất là 5.
(III) Hàm số f x = tan x tuần hoàn với chu kì 2 π .
(IV) Hàm số f x = cos x đồng biến trên khoảng 0 ; π .
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 4.
B. 2.
C. 3.
D. 1.
Một vật chuyển động tròn đều với vận tốc góc là π (rad/s). Hình chiếu của vật trên một đường kính dao động điều hòa với tần số góc, chu kì và tần số bằng bao nhiêu?
A. π rad/s; 2s; 0,5 Hz ; B. 2π rad/s; 0,5 s; 2 Hz
C. 2π rad/s; 1s; 1Hz ; D. π/2 rad/s; 4s; 0,25 Hz
Chọn đáp án A.
Vận tốc góc ω = π rad/s
=> Tần số góc của dao động điều hòa tương ứng là ω = π (rad/s)
Đúng 0
Bình luận (0)
Một chất điểm dao động điều hoà (dạng hàm cos) có chu kì T, biên độ A. Tốc độ trung bình của chất điểm khi pha của dao động biến thiên từ
-
2
π
/
3
đến
π
/
3
bằng A. 3A/T B. 4A/T C. 3,6A/T D. 2A/T
Đọc tiếp
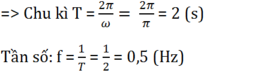
Một chất điểm dao động điều hoà (dạng hàm cos) có chu kì T, biên độ A. Tốc độ trung bình của chất điểm khi pha của dao động biến thiên từ - 2 π / 3 đến π / 3 bằng
A. 3A/T
B. 4A/T
C. 3,6A/T
D. 2A/T
Tìm txđ của các hàm số sau
1. y = tan ( x - 2π/3)
2. y = cot ( x + π/6)
3. y = sin căn 1+x/ 2-x
ĐKXĐ:
a. \(cos\left(x-\dfrac{2\pi}{3}\right)\ne0\Rightarrow x-\dfrac{2\pi}{3}\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{6}+k\pi\)
b. \(sin\left(x+\dfrac{\pi}{6}\right)\ne0\Rightarrow x+\dfrac{\pi}{6}\ne k\pi\Rightarrow x\ne-\dfrac{\pi}{6}+k\pi\)
c. \(\dfrac{1+x}{2-x}\ge0\Rightarrow-1\le x< 2\)
Đúng 1
Bình luận (0)
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π/2 bằng:
A. 1; B. 2/7;
C. 2π; D. 2π/3.
Đáp án: D.
Hướng dẫn: Thể tích khối tròn xoay này được tính bởi
Đúng 0
Bình luận (0)
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:42
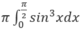
Đồ thị của các hàm số y=sinx và y=cosx cắt nhau tại bao nhiêu điểm có hoành độ thuộc đoạn [−2π;`(5π)/2`]
?
A. 5 B. 6 C. 4 D. 7
Một vật chuyển động tròn đều với tốc độ góc là π rad/s. Hình chiếu của vật trên một đường kính dao động điều hòa với tần số góc, chu kì và tần số bằng bao nhiêu?
A. π rad/s; 2 s; 0,5 Hz.
B. 2π rad/s; 0,5 s; 2 Hz.
C. 2π rad/s; 1 s; 1 Hz.
D. π/2 rad/s; 4 s; 0,25 Hz.
A.
Tần số góc bằng tốc độ góc: ω = π (rad/s).
Chu kì: T = = 2 s; Tần số: f =
= 0,5 Hz.
Đúng 0
Bình luận (0)
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
a) y = x – sinx, x ∈ [0; 2π].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2π]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.
Vậy hàm số đồng biến trên đoạn [0; 2π].
c) Xét hàm số y = sin(1/x) với x > 0.
Giải bất phương trình sau trên khoảng (0; + ∞ ):
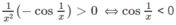
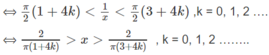
Do đó, hàm số đồng biến trên các khoảng
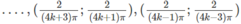
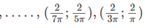
Và nghịch biến trên các khoảng
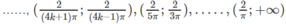
với k = 0, 1, 2 …
Đúng 0
Bình luận (0)
Trong bốn hàm số (1)y=cos2x, (2)y=sinx, (3)y=tan2x, (4)y=cot4x có mấy hàm số tuần hoàn với chu kì là π
A. 3
B. 2
C. 0
D. 1
