Cho hàm số y = tanx – cotx. Khoảng mà hàm số xác định là:
A. 0 ; 2 π \ π 2
B. 0 ; 2 π
C. 0 ; 2 π \ 3 π 2
D. 0 ; 2 π \ π 2 ; π ; 3 π 2
Tập xác định của hàm số y = tan x + c o t x là
A. R
![]()
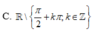
![]()
Xét bốn mệnh đề sau:
1 : Hàm số y = s inx có tập xác định là R
2 : Hàm số y = c osx có tập xác định là R
3 Hàm số y = tan x có tập xác định là R
4 Hàm số y = cot x có tập xác định là R
Tìm số phát biểu đúng.
A. 3
B. 2
C. 4
D. 1
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
Tìm điều kiện xác định của hàm số y = tanx + cotx.
A. x ≠ kπ,k ϵ ℤ.
B. x ≠ π/2,k ϵ ℤ
C. x ≠ kπ/2,k ϵ ℤ
D. x ϵ ℝ
Khẳng định nào sau đây là đúng?
A. Hàm số y = sinx là hàm số chẵn.
B. Hàm số y = cosx là hàm số chẵn
C. Hàm số y = tanx là hàm số chẵn
D. Hàm số y = cotx là hàm số chẵn
Ta có tập xác định của hàm số \(y=cosx\) là \(\mathbb{R}.\)
Nếu với \(x\in\mathbb{R}\) thì \(-x\in\mathbb{R}\) và\(y\left(-x\right)=cos\left(-x\right)=cosx=y\left(x\right).\)
Vậy hàm số \(y=cosx\) là hàm số chẵn.
\(\Rightarrow B\)
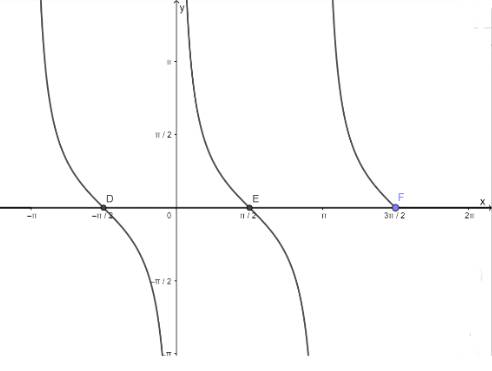
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
a) Hàm số y = tanx nhận giá trị bằng – 1
b) Hàm số y = tanx nhận giá trị bằng 0
c) Hàm số y = cotx nhận giá trị bằng 1
d) Hàm số y = cotx nhận giá trị bằng 0
a) Hàm số y = tanx nhận giá trị bằng – 1
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = tanx và y = - 1
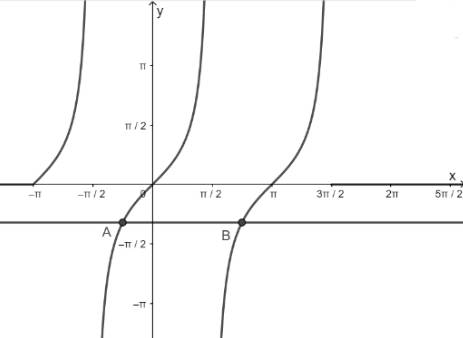
b) Hàm số y = tanx nhận giá trị bằng 0
- Vẽ hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
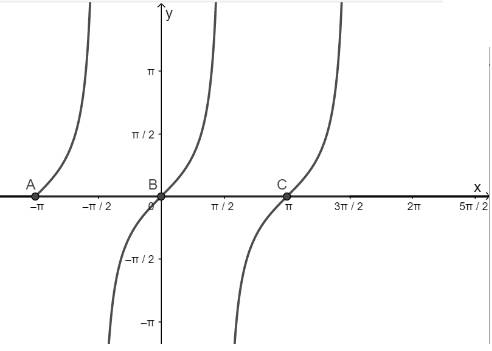
c) Hàm số y = cotx nhận giá trị bằng 1
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = cotx và y = 1
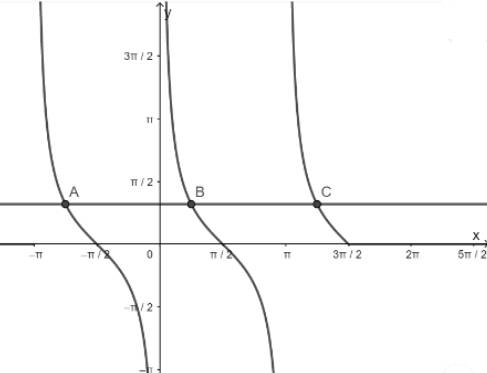
d) Hàm số y = cotx nhận giá trị bằng 0
- Vẽ hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = tanx và y = 0
Hàm số y = tan x − cot x có đạo hàm là
A. y ' = 1 cos 2 2 x
B. y ' = 4 sin 2 2 x
C. y ' = 4 cos 2 2 x
D. y ' = 1 sin 2 2 x
Chọn B
y ' = 1 cos 2 x + 1 sin 2 x = sin 2 x + cos 2 x sin 2 x . cos 2 x = 1 ( s inx. cosx) 2 = 1 sin 2 x 2 2 = 4 sin 2 2 x
Hàm số y = tanx – cotx có đạo hàm là:
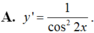
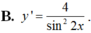
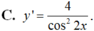
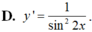
Cho hàm số y = sin x / ( 1 + tan x ) v à k ∈ Z .
Khoảng nào dưới đây không nằm trong tập xác định của hàm số?
A. - π 2 + k 2 π ; π 2 + k 2 π ;
B. π + k 2 π ; 3 π 2 + k 2 π ;
C. 3 π 4 + k 2 π ; 3 π 2 + k 2 π ;
D. π 2 + k 2 π ; 3 π 4 + k 2 π ;
Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = m (Hình 37)
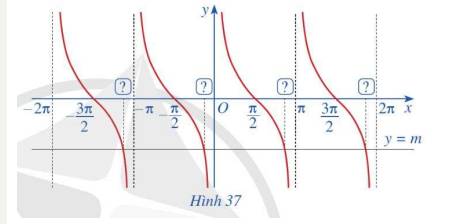
a) Từ hoành độ giao điểm của đồ thị hàm số y = cotx và đường thẳng y = m trên khoảng \(\left( {0;\pi } \right)\), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó.
b) Có nhận xét gì về nghiệm của phương trình cotx = m?
a) Do hoành độ giao điểm nằm trên khoảng \(\left( {0;\pi } \right)\) nên: \(\cot x = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng\(\left( {0;\pi } \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)