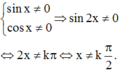Các câu hỏi tương tự
Trong các hàm số
y
tan
x
;
y
sin
2
x
;
y
sin
x
;
y
c
o
t
x
có bao nhiêu hàm số thỏa mãn tính chất
f
x
+
k
π
f...
Đọc tiếp
Trong các hàm số y = tan x ; y = sin 2 x ; y = sin x ; y = c o t x có bao nhiêu hàm số thỏa mãn tính chất f x + k π = f x ; ∀ x ∈ ℝ ; k ∈ ℤ
A. 3
B. 2
C. 1
D. 4
Cho sinα.cos(α+β) = sinβ với α+β ≠ π/2 + kπ,α ≠ π/2+lπ(k,l ϵ Z). Ta có:
A. tan(α+β)=2cotα
B. tan(α+β)=2cotβ
C. tan(α+β)=2tanβ
D.tan(α+β)=2tanα
Cho A = {x ϵ ℤ, -4≤ x ≤5} và B = {0;1;2;3} Tìm A\B ?
A. A\B={-4;-3;-2;-1;4;5}
B. A\B={-3;-2;-1;4;}
C. A\B={-4;-3;-2;-1;0;1;2;3;4;5}
D. A\B={0;1;2;3}
Phương trình sin x -3 cos x 0 có nghiệm dạng
x
a
r
c
cot
m
+
k
π
,
k
∈
ℤ
thì giá trị m là? A. m -3 B.
m
1
3
C. m 3 D. m 5
Đọc tiếp
Phương trình sin x -3 cos x = 0 có nghiệm dạng x = a r c cot m + k π , k ∈ ℤ thì giá trị m là?
A. m = -3
B. m = 1 3
C. m = 3
D. m = 5
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;10), N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y) với x,y ϵ ℤ nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm A(x;y)ϵS Xác suất để x+y ≤ 90 bằng: A. 845/1111 B. 473/500 C. 169/200 D. 86/101
Đọc tiếp
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;10), N(100;10) và P(100;0). Gọi S là tập hợp tất cả các điểm A(x;y) với x,y ϵ ℤ nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm A(x;y)ϵS Xác suất để x+y ≤ 90 bằng:
A. 845/1111
B. 473/500
C. 169/200
D. 86/101
Cho hàm số
f
x
0
k
h
i
x
π
2
+
k
π...
Đọc tiếp
Cho hàm số f x = 0 k h i x = π 2 + k π , k ∈ ℤ 1 2 + tan 2 x
Tìm điều kiện của a để hàm số g x = f x + f a x tuần hoàn
A. a ∈ Z
B. a ∈ Q
C. a ∈ N
D. a ∈ 0 ; + ∞
Cho hàm số f liên tục trên ℝ thỏa mãn
f
x
+
f
-
x
2
+
2
cos
2
x
, với mọi x ϵ ℝ. Giá trị của tích phân
I
∫
-
π
2
π
2
là...
Đọc tiếp
Cho hàm số f liên tục trên ℝ thỏa mãn f x + f - x = 2 + 2 cos 2 x , với mọi x ϵ ℝ. Giá trị của tích phân I = ∫ - π 2 π 2 là
A. -2
B. -7
C. 7
D. 2
Cho hàm số f(x) thỏa mãn f(1) 1/3 và
f
x
x
f
x
2
với mọi x ϵ ℝ. Giá trị f(2) bằng A. 16/3 B. 3/16 C. 2/3 D. 3/2
Đọc tiếp
Cho hàm số f(x) thỏa mãn f(1) = 1/3 và f ' x = x f x 2 với mọi x ϵ ℝ. Giá trị f(2) bằng
A. 16/3
B. 3/16
C. 2/3
D. 3/2
Cho hàm số f(x) liên tục trên R thoả mãn
f
(
t
a
n
x
)
c
o
s
4
x
,
∀
x
∈
R
{
π
2
+
k
π
,
k
∈
Z
}
. Tích phân
∫
0
1
f
(
x
)...
Đọc tiếp
Cho hàm số f(x) liên tục trên R thoả mãn f ( t a n x ) = c o s 4 x , ∀ x ∈ R \ { π 2 + k π , k ∈ Z } . Tích phân ∫ 0 1 f ( x ) d x bằng
A. π + 2 8
B. 1
C. π + 2 4
D. π 4
Có bao nhiêu giá trị nguyên của m ϵ (-15;15) sao cho hàm số
y
tan
x
-
10
tan
x
-
m
đồng biến trên khoảng (0;π/4)? A. 20 B. 9 C. 10 D. 29
Đọc tiếp
Có bao nhiêu giá trị nguyên của m ϵ (-15;15) sao cho hàm số y = tan x - 10 tan x - m đồng biến trên khoảng (0;π/4)?
A. 20
B. 9
C. 10
D. 29