Cho a, b, c là các số dương thỏa điều kiện : a + b + c = 1 . Tìm giá trị nhỏ nhất của biểu thức:
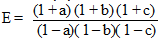
Cho a, b, c là các số dương thỏa mãn điều kiện a+b+c=1. Tìm giá trị nhỏ nhất của biểu thức \(B=\frac{\left(1+a\right)\left(1+b\right)\left(1+c\right)}{\left(1-a\right)\left(1-b\right)\left(1-c\right)}\)
cho a,b,c là các số dương thỏa mãn điều kiện a + b + c = 1
Tìm giá trị nhỏ nhất của biểu thức A = \(\frac{\left(1+a\right)\left(1+b\right)\left(1+c\right)}{\left(1-a\right)\left(1-b\right)\left(1-c\right)}\)
a + b + c= 1 \(\Rightarrow\)1 - a = b + c > 0
Tương tự : 1 - b > 0 ; 1 - c > 0
Mà 1 + a = 1 + ( 1 - b - c ) = ( 1- b ) + ( 1 - c ) \(\ge\)\(2\sqrt{\left(1-b\right)\left(1-c\right)}\)
Tương tự : \(1+b\ge2\sqrt{\left(1-a\right)\left(1-c\right)}\); \(1+c\ge2\sqrt{\left(1-a\right)\left(1-b\right)}\)
\(\Rightarrow\left(1+a\right)\left(1+b\right)\left(1+c\right)\ge8\sqrt{\left(1-a\right)^2\left(1-b\right)^2\left(1-c\right)^2}=8\left(1-a\right)\left(1-b\right)\left(1-c\right)\)
\(\Rightarrow A=\frac{\left(1+a\right)\left(1+b\right)\left(1+c\right)}{\left(1-a\right)\left(1-b\right)\left(1-c\right)}\ge8\)
Dấu " = : xảy ra \(\Leftrightarrow a=b=c=\frac{1}{3}\)
Vậy GTNN của A là 8 \(\Leftrightarrow a=b=c=\frac{1}{3}\)
Cách khác:
\(A=\frac{\left[\left(a+b\right)+\left(a+c\right)\right]\left[\left(b+c\right)+\left(b+a\right)\right]\left[\left(c+a\right)+\left(c+b\right)\right]}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
Áp dụng BĐT Cô si cho 2 số ta được:
\(A\ge\frac{8\sqrt{\left(a+b\right)^2\left(b+c\right)^2\left(c+a\right)^2}}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=8\)
"=" <=> a = b = c = 1/3
Kết luận..
Cho các số thực dương a,b,c thỏa mãn điều kiện \(a+b+c\le\frac{3}{2}\).Tìm giá trị nhỏ nhất của biểu thức \(M=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
tích mình đi
làm ơn
rùi mình
tích lại
thanks
Áp dụng BĐT bunhiacopxki ta có :\(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge\left(\sqrt{a}.\frac{1}{\sqrt{a}}+\sqrt{b}.\frac{1}{\sqrt{b}}+\sqrt{c}.\frac{1}{\sqrt{c}}\right)^2\)
\(\Rightarrow\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge\left(1+1+1\right)^2=9\)
.Dấu "=" xảy ra khi :\(\frac{a}{\frac{1}{a}}=\frac{b}{\frac{1}{b}}=\frac{c}{\frac{1}{c}}\Leftrightarrow a^2=b^2=c^2\Leftrightarrow a=b=c\)
Mà \(a+b+c\le\frac{3}{2}\)\(\Rightarrow M=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge9:\frac{3}{2}=9.\frac{2}{3}=6\)
Vậy Min M = 6 <=> a = b = c
Cho a,b là các số dương thỏa mãn a+b+c=1.Tìm giá trị nhỏ nhất của biểu thức A= a*b+2*b*c+3*c
bạn kiểm tra lại xem có sai đề không
Cho a,b là các số dương thỏa mãn a+b+c=1.Tìm giá trị nhỏ nhất của biểu thức A= a*b+2*b*c+3*c
Xét các số thực âm a,b,c thay đổi thỏa mãn điều kiện 4(ab+bc+ac)=9abc+1 tìm giá trị nhỏ nhất của biểu thức P=a+b+c
Ủa số thực âm hay không âm vậy em?
Đặt \(a+b+c=p\) ; \(ab+bc+ca=q\) ; \(abc=r\)
\(\Rightarrow p^2\ge3q\)
Từ giả thiết: \(4q=9r+1\)
Áp dụng BĐT Schur bậc 3: \(r\ge\dfrac{4pq-p^3}{9}\)
\(\Rightarrow4q\ge4pq-p^3+1\Leftrightarrow p^3-1+4q-4pq\ge0\)
\(\Leftrightarrow\left(p-1\right)\left(p^2+p+1-4q\right)\ge0\)
Nếu \(p< 1\Rightarrow p^2+p+1-4q\le0\)
Mà \(p< 1\Rightarrow1>p^2\Rightarrow0\ge p^2+p+1-4q>p^2+p+p^2-4q\)
\(\Rightarrow2\left(p^2-2q\right)+p< 0\) (vô lý do \(p^2\ge3q\ge2q\))
\(\Rightarrow p\ge1\)
Vậy \(P_{min}=1\) khi \(a=b=c=\dfrac{1}{3}\) hoặc \(\left(a;b;c\right)=\left(\dfrac{1}{2};\dfrac{1}{2};0\right)\) và các hoán vị
Câu 11: (0,5 điểm).
Cho các số thực dương a b, thỏa mãn điều kiện ab 6 và b 3 . Tìm giá trị nhỏ nhất của
biểu thức : P a b 2016
ab>=6 và b>= 3 nha
P=a+b+2016
các bạn giúp mk ik
cám ơn rất nhiều
Cho a,b là các số dương thỏa mãn a+b+c=1.
Tìm giá trị nhỏ nhất của biểu thức A= a*b+2*b*c+3*c*a