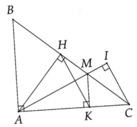
Cho HCN ABCD.H là hình chiếu của B trên cạnh AC;Gọi E;F;M;N lần lượt là trung điểm của AB,DH,HC,AD.Cm:EF vuông góc MN

Những câu hỏi liên quan
cho hình bình hành abcd.H,K lần lượt là hình chiếu của a và c lên cạnh bd chứng minh rằng tam giác ahd=tam giác ckb b tứ giác ahck là hình bình hành
Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔAHD=ΔCKB
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó:AHCK là hình bình hành
Đúng 0
Bình luận (0)
Cho HCN ABCD có AB=12cm, BC=5cm. Gọi H là hình chiếu vuông góc của B trên AC. Tính AC, HA, HC
Xét tam giác ABC vuông tại B ta có:
\(AB^2+BC^2=AC^2\)
\(\Leftrightarrow12^2+5^2=AC^2\)
\(\Leftrightarrow AC^2=169\)
\(\Leftrightarrow AC=13cm\)
Xét tam giác ABC vuông tại H, đường cao BH:
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(AB^2=AH.AC\)
\(\Leftrightarrow12^2=AH.13\)
\(\Leftrightarrow144=AH.13\)
\(\Leftrightarrow AH=\dfrac{144}{13}cm\)
\(HC=AC-AH\)
\(\Leftrightarrow HC=13-\dfrac{144}{13}\)
\(\Leftrightarrow HC=\dfrac{25}{13}cm\)
Đúng 2
Bình luận (0)
Cho hcn ABCD, h là hình chiếu của B trên AC. E,F,M,N lần lượt là trg đ của AB, DH, HC,AD.
CMR : EF vuông góc MN
Cho hcn ABCD . Trên đường chéo BD lấy P .GỌi M là điểm đoi xung của C qua P.
a, tứ giác AMDB là hình j ?
b, Gọi E và F lần lượt là hình chiếu của M lên AD và AB .CM EF // AC và ba điểm E,F,P thẳng hàng
c, cm tỉ số các cạnh của hcn MEFA ko phụ thuộc vào vị trí của P
d, Giả sử CP vuong góc vs BD và CP=2,4 cm ,PD/PB =9/16 Tính các cạnh hcn ABCD
Cho tam giac abc vuong tai a co goc B>goc C .Gọi H là hình chiếu đỉnh A trên cạnh BC.Trên tia HC lấy D sao cho HB=HD(D thuộc BC)Gọi E là hình chiếu D trên cạnh AC .K là hình chiếu của C trên đường thẳng AD.Cmr:
a)D nằm trên HC
b)DE=DK
Trong không gian Oxyz, cho tam giác ABC có các đỉnh B, C thuộc trục Ox. Gọi
E
6
;
4
;
0
,
F
1
;
2
;
0
lần lượt là hình chiếu của B và C trên các cạnh AC, AB. Tọa độ hình chiếu của A trên BC là: A.
8
3...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC có các đỉnh B, C thuộc trục Ox. Gọi E 6 ; 4 ; 0 , F 1 ; 2 ; 0 lần lượt là hình chiếu của B và C trên các cạnh AC, AB. Tọa độ hình chiếu của A trên BC là:
A. 8 3 ; 0 ; 0
B. 5 3 ; 0 ; 0
C. 7 2 ; 0 ; 0
D. 2 ; 0 ; 0
Phương pháp:
- Gọi D là hình chiếu của A lên BC.

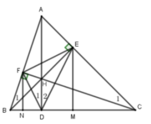
Gọi N, D, M lần lượt là hình chiếu của F, A, E lên BC. H là trực tâm tam giác.


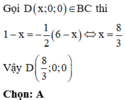
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A; đường cao AH. Gọi K, D lần lượt là hình chiếu của H trên các cạnh AB, AC; I là trung điểm AH. C/m rằng a, Tứ giác AKHD là hcn b,K đối xứng với D qua I c, Gọi M là trung điểm BC. C/m góc BAH = góc CM d, C/m KD vuông góc AM e, Gọi E, F lần lượt là trung điểm BH và CK. C/m KE song song DF
Cho tứ giác ABCD nội tiếp đường tròn (O) có hai đường chéo AC và BD vuông góc với nhau tại I.Gọi E,F,G,H lần lượt là trung điểm của các cạnh AB, BC,CD,AD.C/m
1) tứ giác EFGH là hcn
2) GIEO là hbh
3)hình chiếu của điểm I trên các cạnh và trung điểm của các cạnh của tứ giác ABCD cùng nằm trên một đường tròn
Cho tam giác ABC vuông tại A (AB AC), đường cao AH. Trên cạnh BC lấy điểm M sao cho BA BM. .a) Chứng minh AM là tia phân giác của
H
A
C
^
.b) Gọi K là hình chiếu vuông góc của M trên AC. Chứng minh AM là trung trực của HK.c) Gọi I là hình chiếu vuông góc của C trên tia AM. Chứng minh AH, KM, CI đồng quy.d) Chứng minh AB + AC AH + B
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Trên cạnh BC lấy điểm M sao cho BA = BM. .
a) Chứng minh AM là tia phân giác của H A C ^ .
b) Gọi K là hình chiếu vuông góc của M trên AC. Chứng minh AM là trung trực của HK.
c) Gọi I là hình chiếu vuông góc của C trên tia AM. Chứng minh AH, KM, CI đồng quy.
d) Chứng minh AB + AC < AH + B