Phương pháp:
- Gọi D là hình chiếu của A lên BC.

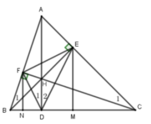
Gọi N, D, M lần lượt là hình chiếu của F, A, E lên BC. H là trực tâm tam giác.


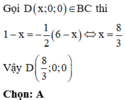
Phương pháp:
- Gọi D là hình chiếu của A lên BC.


Gọi N, D, M lần lượt là hình chiếu của F, A, E lên BC. H là trực tâm tam giác.


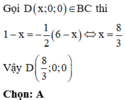
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số y = log a x , y = log a x , y = log a 3 x , với (x>0;a>1). Giá trị của a là
A. a = 6 3
B. a = 6 6
C. a = 3
D. a = 3 6
Trong không gian Oxyz , cho hai mặt phẳng P : 2 x - y + 2 z + 5 = 0 và Q : x - y + 2 = 90 . Trên (P) có tam giác ABC , gọi A ' , B ' , C ' lần lượt là hình chiếu của A,B,C trên (Q) . Biết tam giác ABC có diện tích bằng 4, tính diện tích tam giác A ' B ' C '
A. 2
B. 2 2
C. 2
D. 4 2
Trong không gian Oxyz, cho tam giác ABC có các đỉnh B và C trên các cạnh AC, AB. Tọa độ hình chiếu A trên BC là
A. (2;0;0)
B. 5 3 ; 0 ; 0
C. 7 2 ; 0 ; 0
D. 8 3 ; 0 ; 0
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; 0; 2), B(3; 0; 5), C(1; 1; 0). Tọa độ của điểm D sao cho ABCD là hình bình hành là
A. D(4; 1; 3)
B. D(-4; -1; -3)
C. D(2; 1; -3)
D. D(-2; 1; -3)
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD có diện tích bằng 36, đường thẳng chứa cạnh AB song song với trục Ox, các đỉnh A, B và C lần lượt nằm trên đồ thị các hàm số y = log a x , y = log a x , y = log a 3 x , với x > 0 , a > 1 . Giá trị của a là:
A. a = 6 3
B. a = 6 6
C. a = 3
D. a = 3 6
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( α ) : bc . x + ac . y + ab . z - abc = 0 với a, b, c là các số khác 0 thỏa mãn 1 a + 2 b + 3 c = 7 . Gọi A, B, C lần lượt là giao điểm của α với các trục tọa độ Ox, Oy, Oz. Biết mặt phẳng α tiếp xúc với mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 72 7 . Thể tích khối OABC với O là gốc tọa độ bằng
A. 2 9
B. 3 4
C. 1 8
D. 4 3
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 2 1 = y - 2 2 = z + 2 - 1 và mặt phẳng ( α ) :2x+2y-z-4=0. Tam giác ABC có A(-1;2;1), các đỉnh B, C nằm trên (α) và trọng tâm G nằm trên đường thẳng d. Tọa độ trung điểm M của BC là
A. M(2;1;2)
B. M(0;1;-2)
C. M(1;-1;-4)
D. M(2;-1;-2)
Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD có diện tích bằng 16. Biết tam giác ABC cân tại A, cạnh BC=4 và K ( 21 5 ; 18 5 ) là hình chiếu của điểm B xuống AC. Tìm tọa độ điểm D biết rằng điểm B thuộc đường thẳng △ : x + y - 3 = 0 đồng thời hoành độ các điểm B, C đều là các số nguyên
A. D(5;2)
B. D(7;6)
C. (-7;-6)
D. D(-5;-2)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(a;b;c), (a > 0) thuộc đường thẳng d : x − 3 = y + 2 − 1 = z − 1 2 . Hình chiếu song song của điểm M trên mặt phẳng P : x + 5 y − 2 = 0 theo phương của đường thẳng Δ: x = 3 − t y = 1 + 2 t z = − 3 t là điểm M’ sao cho MM ' = 14 . Tính giá trị của biểu thức T = a + b + c là:
A. 0
B. 1
C. 2
D. 3