Tính bán kính của mặt cầu ngoại tiếp hình tứ diện đều cạnh a.
A. a 3 2
B. a 6 2
C. a 6 4
D. a 2 4
II. Tự luận ( 4 điểm)
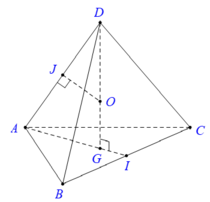
Tính bán kính của mặt cầu ngoại tiếp hình tứ diện ABCD đều cạnh a.
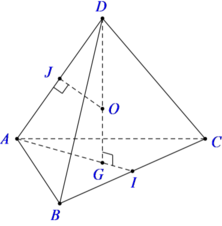
Gọi I là trung điểm cạnh BC, G là trọng tâm của tam giác ABC.

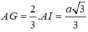 và DG là trục của tam giác ABC.
và DG là trục của tam giác ABC.
Trong mp (DAG), kẻ trung trực của DA cắt DG tại O thì: OD = OA = OB = OC nên O chính là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Bán kính R của mặt cầu bằng độ dài đoạn OD.
Trong tam giác ADG vuông tại G, ta có:
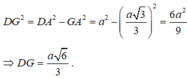
Mặt khác, tam giác DJO đồng dạng tam giác DGA nên:
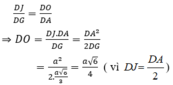
Vậy bán kính của mặt cầu ngoại tiếp hình tứ diện ABCD đều cạnh a là R = a 6 4
Tính bán kính R mặt cầu ngoại tiếp tứ diện đều ABCD cạnh a 2
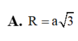
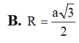
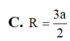
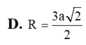
Bán kính của mặt cầu ngoại tiếp tứ diện đều cạnh a là
A. a 3 4 .
B. a 6 4 .
C. a 2
D. 2 a 3
Đáp án B.
![]()
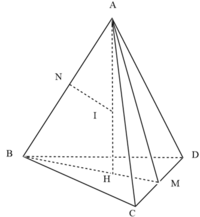
M là trung điểm của CD; N là trung điểm của AB.
Trong mặt phẳng (ABM), kẻ đường thẳng qua N, vuông góc với AB, cắt AH tại I. Khi đó, I là tâm đường tròn ngoại tiếp tứ diện ABCD.
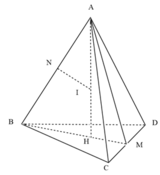
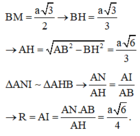
Bán kính của mặt cầu ngoại tiếp tứ diện đều cạnh a là
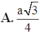
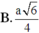
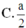
Đáp án B.
H là tâm của ΔBCD → A H ⊥ ( B C D ) . M là trung điểm của CD; N là trung điểm của AB.
Trong mặt phẳng (ABM), kẻ đường thẳng qua N, vuông góc với AB, cắt AH tại I. Khi đó, I là tâm đường tròn ngoại tiếp tứ diện ABCD
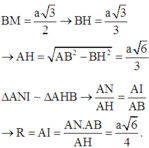
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
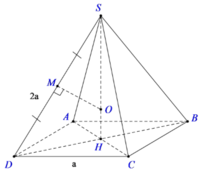
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông ABCD.
Gọi M là trung điểm của SD, trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O. Suy ra; OS = OD (1)
Mà O thuộc trục SH của hình vuông ABCD nên:
OA = OB = OC = OD (2)
Từ (1) và (2) suy ra: OA = OB = OC = OD = OS
Do đó, O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD. Bán kính mặt cầu là R = SO
Ta có:
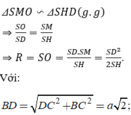
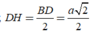
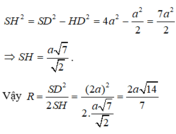
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
A. 2 a 14 7
B. 2 a 7 2
C. 2 a 7 3 2
D. 2 a 2 7
Đáp án A
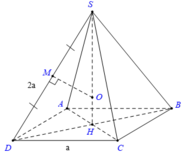
Cho hình chóp tứ giác đều S.ABCD.
Gọi H là tâm đáy thì SH là trục của hình vuông.
Gọi M là trung điểm của ABCD .
Trong mp (SDH) kẻ trung trực của đoạn SD cắt SH tại O
Thì OS = OA = OC = OD
Nên O chính là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD .
Bán kính mặt cầu là R = SO.
Ta có:
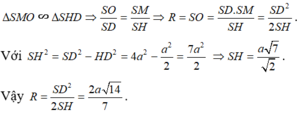
Hình tứ diện ABCD có các mặt ABC và BCD là tam giác đều cạnh a, góc giữa đường thẳng AD và mp(ABC) bằng 45 độ. Tính bán kính mặt cầu ngoại tiếp tứ diện.
Gọi E là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}AE\perp BC\\DE\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ADE\right)\)
Trong tam giác cân ADE (cân tại E), kẻ \(DH\perp AE\Rightarrow DH\perp\left(ABC\right)\)
\(\Rightarrow\widehat{DAE}=45^0\Rightarrow\Delta ADE\) vuông cân tại E
Gọi G và G' lần lượt là trọng tâm ABC và BCD. Trong mp (ADE), qua G kẻ đường thẳng d song song DE, qua G' kẻ d' song song AE. Gọi O là giao điểm d và d' \(\Rightarrow\) O là tâm mặt cầu ngoại tiếp tứ diện
Ta có: \(AE=DE=\dfrac{a\sqrt{3}}{2}\) ; \(AG=\dfrac{2}{3}AE=\dfrac{a\sqrt{3}}{3}\) ; \(OG=OG'=\dfrac{1}{3}AE=\dfrac{a\sqrt{3}}{6}\)
\(R=OA=\sqrt{AG^2+OG^2}=\dfrac{a\sqrt{15}}{6}\)
Hình chóp tứ giác đều có tất cả các cạnh bằng a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp.
A. R = a
B. R = a 2
C. R = a 2 2
D. R = a 3 2
Cho tứ diện đều ABCD cạnh a. Gọi K là trung điểm của AB, M, N lần lượt là hình chiều của K lên AD và AC. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp K.CDMN?
![]()
![]()