Đáp án B.
![]()
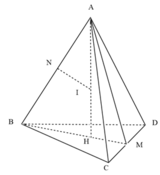
M là trung điểm của CD; N là trung điểm của AB.
Trong mặt phẳng (ABM), kẻ đường thẳng qua N, vuông góc với AB, cắt AH tại I. Khi đó, I là tâm đường tròn ngoại tiếp tứ diện ABCD.
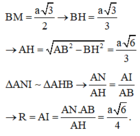
Đáp án B.
![]()
M là trung điểm của CD; N là trung điểm của AB.
Trong mặt phẳng (ABM), kẻ đường thẳng qua N, vuông góc với AB, cắt AH tại I. Khi đó, I là tâm đường tròn ngoại tiếp tứ diện ABCD.

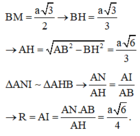
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có các cạnh A B = a , A D = 2 a , A A ' = 3 a . Tìm bán kính của mặt cầu ngoại tiếp tứ diện CB′C′D′.
A. 3 a 2 .
B. 14 a 2 .
C. 3 a
D. 7 a 2 .
Cho tứ diện đều ABCD có cạnh a. Một mặt cầu tiếp xúc với các mặt của tứ diện có bán kính là:
A. a 6 12
B. a 6 6
C. a 6 3
D. a 6 8
Cho lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều cạnh bằng a, góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30 o . Biết hình chiếu vuông góc của A’ trên (ABC)trùng với trung điểm cạnh BC. Tính theo a bán kính mặt cầu ngoại tiếp tứ diện A'.ABC
A. R = a 3 9
B. R = 2 a 3 3
C. R = a 3 3
D. R = a 3 6
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều có cạnh bằng a, cạnh bên tạo với đáy góc 300. Biết hình chiếu vuông góc của A’ trên trùng với trung điểm cạnh BC. Tính bán kính mặt cầu ngoại tiếp tứ diện A’ABC.
A. a 3
B. a 3 2
C. a 3 6
D. a 3 3
Trong không gian Oxyz. Cho tứ diện đều ABCD có A(0;1;2) và hình chiếu vuông góc của A trên mặt phẳng (BCD) là H (4; -3;-2). Tọa độ tâm I của mặt cầu ngoại tiếp tứ diện ABCD.
A. I(3; -2;-1).
B. I(2;-1;0).
C. I(3; -2;1).
D. I(-3; -2;1).
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc A B C ^ = 60 ° , cạnh bên SA=a và vuông góc với mặt đáy. Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ACD
A. R = a 5 2
B. R = a
C. R = a 7 12
D. R = a 2
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S).
A. R = a 5
B. R = a 6 3
C. R = a 6 5
C. R = a 3
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, c và tiếp xúc với đường thẳng AD tại A. Tính bán kính R của mặt cầu (S).
A. R = a 6
B. R = a 6 3
C. R = a 6 5
D. R = a 3
Cho hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều cạnh a, cạnh a 2 2 . Gọi D là điểm đối xứng của B qua C. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABD.
A. R = a 39 7
B. R = a 35 7
C. R = a 37 6
D. R = a 39 6