Đáp án B.
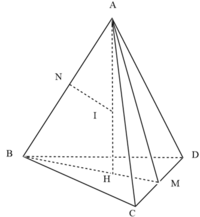
H là tâm của ΔBCD → A H ⊥ ( B C D ) . M là trung điểm của CD; N là trung điểm của AB.
Trong mặt phẳng (ABM), kẻ đường thẳng qua N, vuông góc với AB, cắt AH tại I. Khi đó, I là tâm đường tròn ngoại tiếp tứ diện ABCD
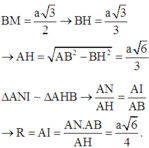
Đáp án B.
H là tâm của ΔBCD → A H ⊥ ( B C D ) . M là trung điểm của CD; N là trung điểm của AB.
Trong mặt phẳng (ABM), kẻ đường thẳng qua N, vuông góc với AB, cắt AH tại I. Khi đó, I là tâm đường tròn ngoại tiếp tứ diện ABCD

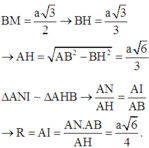
Cho tứ diện ABCD có AB =4a, CD= 6a, các cạnh còn lại đều bằng a 22 .Tính bán kính của mặt cầu ngoại tiếp tứ diện ABCD.
A. 5 a 2
B. 3a
C. a 85 3
D. a 79 3
Cho lăng trụ tam giác đều ABC. A’B’C’ có độ dài cạnh đáy bằng 3a và chiều cao bằng 8a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện AB’C’C.
A. R = 4a.
B. R =5a.
![]()
![]()
Cho tứ diện đều ABCD, A A 1 là một đường cao của tứ diện. Gọi I là trung điểm của A A 1 Mặt phẳng (BCI) chia tứ diện đã cho thành hai tứ diện. Tính tỉ số hai bán kính của hai mặt cầu ngoại tiếp hai tứ diện đó
A. 43 51
B. 1 2
C. 1 4
D. 48 153
Cho tứ diện đều ABCD có cạnh 2a. Tính bán kính r của mặt cầu tiếp xúc với tất cả các mặt của tứ diện.
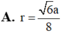
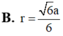
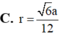
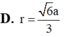
Cho tứ diện ABCD có AB=4a, CD=6a các cạnh còn lại có độ dài bằng a 22 Tính bán kính của mặt cầu ngoại tiếp tứ diện ABCD
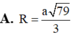
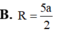
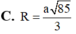
![]()
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 3 2 a cạnh bên bằng 5a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD.
![]()
![]()
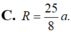
![]()
Tính bán kính mặt cầu ngoại tiếp khối chóp tứ giác đều có cạnh đáy bằng 1 và góc giữa cạnh bên và mặt đáy bằng 60 o
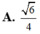

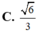
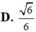
Cho khối tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và OA = OB = OC = 6. Tính bán kính R mặt cầu ngoại tiếp tứ diện OABC.
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có tam giác ABC là tam giác cân với BAC= 120 o ,AB=AC=a Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là V = a 3 16

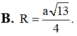
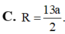
![]()