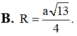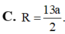Các câu hỏi tương tự
Cho tứ diện ABCD có ABC là tam giác cân tại A, người ta để một quả cầu có bán kính r 1 vào bên trong tứ diện từ đáy ABC sao cho các cạnh AB, BC, CA lần lượt tiếp xúc với quả cầu và phần quả cầu bên trong tứ diện có thể tích bằng phần quả cầu bên ngoài tứ diện. Biết khoảng cách từ D đến (ABC) bằng 2. Tính thể tích nhỏ nhất của tứ diện ABCD?
Đọc tiếp
Cho tứ diện ABCD có ABC là tam giác cân tại A, người ta để một quả cầu có bán kính r = 1 vào bên trong tứ diện từ đáy ABC sao cho các cạnh AB, BC, CA lần lượt tiếp xúc với quả cầu và phần quả cầu bên trong tứ diện có thể tích bằng phần quả cầu bên ngoài tứ diện. Biết khoảng cách từ D đến (ABC) bằng 2. Tính thể tích nhỏ nhất của tứ diện ABCD?
![]()
![]()
![]()
![]()
Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác vuông tại A,
A
B
a
,
A
C
a
2
Biết rằng góc giữa hai mặt phẳng (AB’C’),(ABC) bằng
60
0
và hình chiếu A lên mặt phẳng (ABC) là trung điểm H của đoạn A’B’. Tính bán kính R của mặt cầu ngoại tiếp tứ diệ...
Đọc tiếp
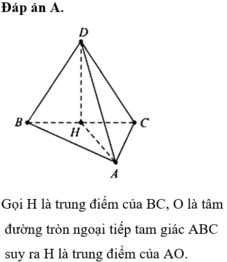
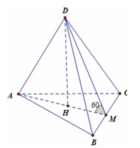
Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác vuông tại A, A B = a , A C = a 2 Biết rằng góc giữa hai mặt phẳng (AB’C’),(ABC) bằng 60 0 và hình chiếu A lên mặt phẳng (A'B'C') là trung điểm H của đoạn A’B’. Tính bán kính R của mặt cầu ngoại tiếp tứ diện AHB’C’
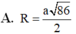
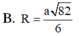

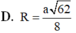
Cho hình tứ diện ABCD có DA BC 5, AB 3, AC 4. Biết DA vuông góc với mặt phẳng (ABC). Thể tích của khối tứ diện ABCD là: a B. V 20 C. V 30 D. V 60
Đọc tiếp
Cho hình tứ diện ABCD có DA = BC = 5, AB = 3, AC = 4. Biết DA vuông góc với mặt phẳng (ABC). Thể tích của khối tứ diện ABCD là:
a
B. V = 20
C. V = 30
D. V = 60
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng
60
O
. Tính thể tích V của khối tứ diện ABCD theo a:
Đọc tiếp
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 O . Tính thể tích V của khối tứ diện ABCD theo a:
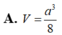
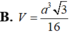
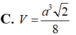
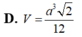
Cho tứ diện ABCD có hai mặt ABC, BCD là các tam giác đều cạnh a và nằm trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là:
Đọc tiếp
Cho tứ diện ABCD có hai mặt ABC, BCD là các tam giác đều cạnh a và nằm trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là:
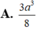
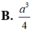
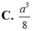
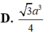
Cho tứ diện ABCD có hai mặt ABC và DBC là những tam giác đều cạnh bằng 1, AD
2
Gọi O là trung điểm cạnh AD. Xét hai khẳng định sau: 1 O là tâm mặt cầu ngoại tiếp tứ diện ABCD. 2 O.ABC là hình chóp tam giác đều. Hãy chọn khẳng định đúng A. Chỉ (2) đúng B. Cả (1) và (2) đều sai. C. Cả (1) và (2) đều đúng D. Chỉ (1) đúng
Đọc tiếp
Cho tứ diện ABCD có hai mặt ABC và DBC là những tam giác đều cạnh bằng 1, AD= 2 Gọi O là trung điểm cạnh AD. Xét hai khẳng định sau:
1 O là tâm mặt cầu ngoại tiếp tứ diện ABCD.
2 O.ABC là hình chóp tam giác đều.
Hãy chọn khẳng định đúng
A. Chỉ (2) đúng
B. Cả (1) và (2) đều sai.
C. Cả (1) và (2) đều đúng
D. Chỉ (1) đúng
Cho tứ diện đều ABCD,
A
A
1
là một đường cao của tứ diện. Gọi I là trung điểm của
A
A
1
Mặt phẳng (BCI) chia tứ diện đã cho thành hai tứ diện. Tính tỉ số hai bán kính của hai mặt cầu ngoại tiếp hai tứ diện đó A.
43
51
B.
1
2
C.
1
4...
Đọc tiếp
Cho tứ diện đều ABCD, A A 1 là một đường cao của tứ diện. Gọi I là trung điểm của A A 1 Mặt phẳng (BCI) chia tứ diện đã cho thành hai tứ diện. Tính tỉ số hai bán kính của hai mặt cầu ngoại tiếp hai tứ diện đó
A. 43 51
B. 1 2
C. 1 4
D. 48 153
Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung đáy BC. Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
b) Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng (BCD).
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD. A.
a
2
3
4
B.
a
2
3
9
C. ...
Đọc tiếp
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD.
A. a 2 3 4
B. a 2 3 9
C. a 2 2 16
D. a 2 3 18