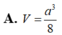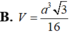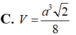Các câu hỏi tương tự
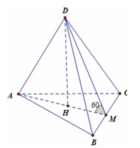
Cho tứ diện ABCD có hai mặt ABC, BCD là các tam giác đều cạnh a và nằm trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là:
Đọc tiếp
Cho tứ diện ABCD có hai mặt ABC, BCD là các tam giác đều cạnh a và nằm trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là:
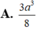
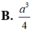
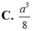
Cho tứ diện ABCD có BD 3, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 11, số đo góc giữa hai mặt phẳng (ABD) và (BCD) là A.
a
r
c
sin
33
40
B.
a
r
c...
Đọc tiếp
Cho tứ diện ABCD có BD =3, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 11, số đo góc giữa hai mặt phẳng (ABD) và (BCD) là
A. a r c sin 33 40
B. a r c sin 11 40
C. a r c cos 33 40
D. a r c cos 11 40
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB 2a.Tan của góc giữa CM với mặt phẳng (BCD) bằng: A.
2
3
3
B.
3
2
C.
2
3
D. không xác định
Đọc tiếp
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa CM với mặt phẳng (BCD) bằng:
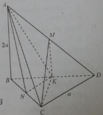
A. 2 3 3
B. 3 2
C. 2 3
D. không xác định
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB 2a.Tan của góc giữa AC với mặt phẳng (ABD) bằng: A.
5
B. 1 C.
51
17
D. Không xác định
Đọc tiếp
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa AC với mặt phẳng (ABD) bằng:
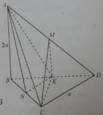
A. 5
B. 1
C. 51 17
D. Không xác định
Cho tứ diện ABCD có ABAD
a
2
, BCBDa, CACDx. Khoảng cách từ B đến mặt phẳng (ACD) bằng
a
3
2
. Biết thể tích của khối tứ diện bằng
a
3
3
12
. Góc giữa hai mặt phẳng (ACD) và (BCD) là A.
60
o...
Đọc tiếp
Cho tứ diện ABCD có AB=AD= a 2 , BC=BD=a, CA=CD=x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A. 60 o
B. 45 o
C. 90 o
D. 120 o
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB 2a.Gọi M là trung điểm của AD và K là trung điểm của BDGóc giữa CM với mặt phẳng (BCD) là: A.
B
C
M
⏜
B.
D
C
M
⏜
C.
K
C
M
⏜
D. ...
Đọc tiếp
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Gọi M là trung điểm của AD và K là trung điểm của BD
Góc giữa CM với mặt phẳng (BCD) là:
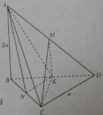
A. B C M ⏜
B. D C M ⏜
C. K C M ⏜
D. A C M ⏜
Cho tứ diện ABCD có AB ⊥ (BCD) và AB=a√3, BCD là tam giác đều cạnh a.Tính góc giữa: 1) AC và (BCD) 2) AD và (BCD) 3) AD và (ABC)
Cho khối tứ diện ABCD có BC3, CD4,
ABC
⏜
B
C
D
⏜
A
D
C
⏜
90...
Đọc tiếp
Cho khối tứ diện ABCD có BC=3, CD=4, ABC ⏜ = B C D ⏜ = A D C ⏜ = 90 o C Góc giữa hai đường thẳng AD và BC bằng 60 o C Côsin góc giữa hai mặt phẳng (ABC) và (ACD) bằng
A. 2 43 43
B. 43 86
C. 2 43 43
D. 43 43
Cho tứ diện ABCD có đáy BCD là tam giác đều, trọng tâm G.
∆
là đường thẳng qua G và vuông góc với (BCD). A chạy trên
∆
sao cho mặt câu ngoại tiếp ABCD có thể tích nhỏ nhất. Khi đó thể tích khối ABCD là:
A
.
a
3
12
B
.
a
3
2...
Đọc tiếp
Cho tứ diện ABCD có đáy BCD là tam giác đều, trọng tâm G. ∆ là đường thẳng qua G và vuông góc với (BCD). A chạy trên ∆ sao cho mặt câu ngoại tiếp ABCD có thể tích nhỏ nhất. Khi đó thể tích khối ABCD là:
A . a 3 12
B . a 3 2 12
C . a 3 3 12
D . a 3 3 6