Giả sử F(x) là một nguyên hàm của hàm số f x = e x x trên khoang 0 ; + ∞ và I = ∫ 1 3 e 3 x x d x . Khẳng định nào sau đây là khẳng định đúng?
A. I = F 3 - F 1
B. I = F 6 - F 3
C. I = F 9 - F 3
D. I = F 4 - F 2
Những câu hỏi liên quan
Giả sử F(x) là nguyên hàm của hàm số f(x)4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là A. (0;-1) B.
5
2
;
8
C.
0
;
-
1
v
à
...
Đọc tiếp
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là
A. (0;-1)
B. 5 2 ; 8
C. 0 ; - 1 v à 5 2 ; 9
D. 5 2 ; 9
f ( x ) = 4 x - 1 ⇒ F ( x ) = ∫ f ( x ) d x = 2 x 2 - x + C
Phương trình hoành độ giao điểm của đồ thị hàm số F(x) và f(x) là:
2 x 2 - x + C = 4 x - 1 ⇔ 2 x 2 - 5 x + C + 1 = 0 ( * )
Do hai đồ thị hàm số trên cắt nhau tại một điểm trên trục tung nên x=0 là nghiệm của (*)
⇔ C + 1 = 0 ⇔ C = - 1
Với C=-1: Phương trình(*)
⇔ 2 x 2 - 5 x = 0 ⇔ [ x = 0 x = 5 2
Tọa độ các điểm chung của hai đồ thị hàm số trên là: (0;-1) và 5 2 ; 9
Chọn đáp án C.
Đúng 0
Bình luận (0)
Giả sử F(x) là nguyên hàm của hàm số f(x)4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
Đọc tiếp
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
Phương pháp:
+) Sử dụng các công thức nguyên hàm cơ bản
xác định hàm số F(x).
+) Giải phương trình hoành độ giao điểm.
Cách giải:
Phương trình hoành độ giao điểm của
đồ thị hàm số F(x) và f(x) là :
Do hai đồ thị hàm số trên cắt nhau tại một
điểm trên trục tung nên x=0 là nghiệm của (*)
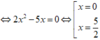
Tọa độ các điểm chung của hai đồ thị
hàm số trên là:
Đúng 0
Bình luận (0)
Giả sử F(x) là một họ nguyên hàm của hàm số
f
(
x
)
sin
x
x
trên khoảng
0
;
+
∞
. Tính tích phân
I
∫
1
3
sin
2
x...
Đọc tiếp
Giả sử F(x) là một họ nguyên hàm của hàm số f ( x ) = sin x x trên khoảng 0 ; + ∞ . Tính tích phân I = ∫ 1 3 sin 2 x x d x
A. F(3) – F(1).
B. F(6) – F(2).
C. F(4) – F(2).
D. F(6) – F(4).
Giả sử hàm số f(x) (ax2 + bx + x)e–x là một nguyên hàm của hàm số g(x) x(1 – x)e–x. Giá trị của biểu thức A a + 2b + 3c bằng A. 3 B. 4 C. 6 D. 9
Đọc tiếp
Giả sử hàm số f(x) = (ax2 + bx + x)e–x là một nguyên hàm của hàm số g(x) = x(1 – x)e–x. Giá trị của biểu thức A = a + 2b + 3c bằng
A. 3
B. 4
C. 6
D. 9
Giả sử F(x) là một nguyên hàm của hàm số
f
(
x
)
1
3
x
+
1
trên khoảng
-
∞
;
-
1
3
. Mệnh đề nào sau đây đúng?
Đọc tiếp
Giả sử F(x) là một nguyên hàm của hàm số f ( x ) = 1 3 x + 1 trên khoảng - ∞ ; - 1 3 . Mệnh đề nào sau đây đúng?
Giả sử hàm số f(x) (ax2 + bx + c).e–x là một nguyên hàm của hàm số g(x) x(1 – x).e–x. Giá trị của biểu thức A a + 2b + 3c bằng A. 6 B. 4 C. 9 D. 3
Đọc tiếp
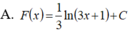
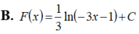
Giả sử hàm số f(x) = (ax2 + bx + c).e–x là một nguyên hàm của hàm số g(x) = x(1 – x).e–x. Giá trị của biểu thức A = a + 2b + 3c bằng
A. 6
B. 4
C. 9
D. 3
Giả sử f(x) là hàm số liên tục trên đoạn [a; b], F(x) và G(x) là hai nguyên hàm của f(x). Chứng minh rằng F(b) – F(a) = G(b) – G(a), (tức là hiệu số F(b) – F(a) không phụ thuộc việc chọn nguyên hàm).
- Vì F(x) và G(x) đều là nguyên hàm của f(x) nên tồn tại một hằng số C sao cho: F(x) = G(x) + C
- Khi đó F(b) – F(a) = G(b) + C – G(a) – C = G(b) – G(a).
Đúng 0
Bình luận (0)
14 tháng 4 2022 lúc 21:36
Cho hàm số fleft(xright)left{{}begin{matrix}2sin^2x+1,x 02^x;xge0end{matrix}right.. Giả sử Fleft(xright) là một nguyên hàm của hàm số fleft(xright) trên R và thỏa mãn điều kiện Fleft(1right)dfrac{2}{ln2}. Tính Fleft(-piright) A. Fleft(-piright)-2pi+dfrac{1}{ln2} B. Fleft(-piright)-2pi-dfrac{1}{ln2}C. Fleft(-piright)-pi-dfrac{1}{ln2} D. Fleft(-piright)-2piMình cần bài giải ạ, mình cảm ơn nhiều ♥
Đọc tiếp
Cho hàm số \(f\left(x\right)=\left\{{}\begin{matrix}2\sin^2x+1,x< 0\\2^x;x\ge0\end{matrix}\right.\). Giả sử \(F\left(x\right)\) là một nguyên hàm của hàm số \(f\left(x\right)\) trên \(R\) và thỏa mãn điều kiện \(F\left(1\right)=\dfrac{2}{ln2}\). Tính \(F\left(-\pi\right)\)
A. \(F\left(-\pi\right)=-2\pi+\dfrac{1}{ln2}\) B. \(F\left(-\pi\right)=-2\pi-\dfrac{1}{ln2}\)
C. \(F\left(-\pi\right)=-\pi-\dfrac{1}{ln2}\) D. \(F\left(-\pi\right)=-2\pi\)
Mình cần bài giải ạ, mình cảm ơn nhiều ♥
Xem thêm câu trả lời
Giả sử F(x) là một họ nguyên hàm của hàm số
f
x
sin
x
x
trên khoảng
0
;
+
∞
. Tính tích phân
∫
1
3
sin
2
x
x...
Đọc tiếp
Giả sử F(x) là một họ nguyên hàm của hàm số f x = sin x x trên khoảng 0 ; + ∞ . Tính tích phân ∫ 1 3 sin 2 x x d x
A. F(3) - F(1)
B. F(6) - F(2)
C. F(4) - F(2)
D. F(6) - F(4)
Đặt t = 2 nên dt = 2dx.
Đổi cận: x = 1 nên t = 2; x = 3 nên t = 6
F x = ∫ sin x x d x ⇒ F u = ∫ sin u u d u ∫ 1 3 sin 2 x x d x = ∫ 1 3 2 sin 2 x 2 x d x ⇒ ∫ 1 3 sin 2 x x d x = ∫ 2 6 sin u u d u = F 6 - F 2
Đáp án B
Đúng 0
Bình luận (0)