Các câu hỏi tương tự
Giả sử hàm số f(x) (ax2 + bx + x)e–x là một nguyên hàm của hàm số g(x) x(1 – x)e–x. Giá trị của biểu thức A a + 2b + 3c bằng A. 3 B. 4 C. 6 D. 9
Đọc tiếp
Giả sử hàm số f(x) = (ax2 + bx + x)e–x là một nguyên hàm của hàm số g(x) = x(1 – x)e–x. Giá trị của biểu thức A = a + 2b + 3c bằng
A. 3
B. 4
C. 6
D. 9
Biết
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của hàm số
f
(
x
)
(
2
x
2
-
5
x
+
2
)
e
-...
Đọc tiếp
Biết F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của hàm số f ( x ) = ( 2 x 2 - 5 x + 2 ) e - x trên ℝ . Giá trị của biểu thức f(F(0)) bằng:
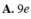
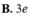
![]()
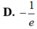
Biết
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của hàm số
f
(
x
)
(
2...
Đọc tiếp
Biết F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của hàm số f ( x ) = ( 2 x 2 - 5 x + 2 ) e - x trên ℝ . Giá trị của biểu thức f(F(0)) bằng
A. 9e
B. - 1 e
C. 3e
D. 20 e 2
Gọi
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
x
là một nguyên hàm của hàm số
f
(
x
)
(
x
-
1
)
2
e
x
. Tính S a...
Đọc tiếp
Gọi F ( x ) = ( a x 2 + b x + c ) e x là một nguyên hàm của hàm số f ( x ) = ( x - 1 ) 2 e x . Tính S= a+2b+c:
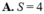
![]()
![]()
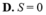
Cho các hàm số:
f
(
x
)
20
x
2
-
30
x
+
7
2
x
-
3
;
F
(
x
)
(
a
x
2
+
b...
Đọc tiếp
Cho các hàm số: f ( x ) = 20 x 2 - 30 x + 7 2 x - 3 ; F ( x ) = ( a x 2 + b x + C ) 2 x - 3 với x > 3 2 . Để F(x) là một nguyên hàm của f(x) thì giá trị của a,b,c lần lượt là:
A. a = 4; b = 2; c= 1
B. a = 4; b = -2; c = -1
C. a = 4; b = -2; c = 1
D. a = 4; b = 2; c = -1 .
Nếu
f
(
x
)
a
x
2
+
b
x
+
c
2
x
-
1
là một nguyên hàm của hàm số
g
(
x
)
10...
Đọc tiếp
Nếu f ( x ) = a x 2 + b x + c 2 x - 1 là một nguyên hàm của hàm số g ( x ) = 10 x 2 - 7 x + 2 2 x - 1 trên 1 2 ; + ∞ thì a+b+c là:
A. 1.
B. 2.
C. 3.
D. 4.
Hàm số
F
(
x
)
a
x
2
+
b
x
+
c
e
x
là một nguyên hàm cùa hàm số
f
x
x
2
e
x
thì a + b + c bằng: A.3. B.1. C.3. D.-2.
Đọc tiếp
Hàm số F ( x ) = a x 2 + b x + c e x là một nguyên hàm cùa hàm số f x = x 2 e x thì a + b + c bằng:
A.3.
B.1.
C.3.
D.-2.
Biết
F
(
x
)
a
ln
|
x
-
1
|
+
b
ln
|
x
-
2
|
(
a
,
b
∈
Z
)
là một nguyên hàm của hàm số
f
(
x
)
x
+...
Đọc tiếp
Biết F ( x ) = a ln | x - 1 | + b ln | x - 2 | ( a , b ∈ Z ) là một nguyên hàm của hàm số f ( x ) = x + 1 ( x - 1 ) ( x - 2 ) . Giá trị của biểu thức b-a bằng
![]()
![]()
![]()
![]()
Biết rằng trên khoảng
3
2
;
+
∞
hàm số
f
(
x
)
20
x
2
-
30
x
+
7
2
x
-
3...
Đọc tiếp
Biết rằng trên khoảng 3 2 ; + ∞ hàm số f ( x ) = 20 x 2 - 30 x + 7 2 x - 3 có một nguyên hàm F ( x ) = ( a x 2 + b x + c ) 2 x - 3 , ( a , b , c ∈ ℤ ) . Tổng S=a+b+c bằng:
A. 6
B. 5
C. 4
D. 3



