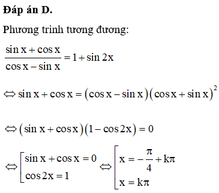Giải phương trình sau: sin2 x + sin2x - 2 cos2 x = 1/2

Những câu hỏi liên quan
giải các phương trình sau : a). sin 2x+sin2 x=1/2
b.2sin2 x +3 sin x cosx + cos2 x= 0
c.sin2 x/2 + sin x - 2 cos 2 x/2 = 1/2
cho phương trình \(\dfrac{1}{sinx}+\dfrac{1}{sin2x}+\dfrac{1}{sin4x}+...+\dfrac{1}{sin2^{2018}x}=0\)
\(\dfrac{1}{sin2k}=\dfrac{sink}{sink.sin2k}=\dfrac{\left(sin2k-k\right)}{sink.sin2k}=\dfrac{sin2k.cosk-cos2k.sink}{sink.sin2k}\)
\(=\dfrac{cosk}{sink}-\dfrac{cos2k}{sin2k}=cotk-cot2k\)
Do đó pt tương đương:
\(cot\dfrac{x}{2}-cotx+cotx-cot2x+...+cot2^{2017}x-cot^{2018}x=0\)
\(\Leftrightarrow cot\dfrac{x}{2}-cot2^{2018}x=0\)
\(\Leftrightarrow\dfrac{x}{2}=2^{2018}x+k\pi\)
\(\Leftrightarrow...\)
Đúng 3
Bình luận (1)
Giải phương trình sau: 3sin2 x – 4 sinx.cosx + 5 cos2 x =2
3sin2x – 4sinx.cosx + 5cos2x = 2
⇔ 3sin2x – 4sinx.cosx + 5cos2x = 2(sin2x + cos2x)
⇔ sin2x – 4sinx.cosx + 3 cos2x = 0 (1)
+ Xét cosx = 0 ⇒ sin2x = 1.
Phương trình (1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0. Chia hai vế phương trình cho cos2x ta được
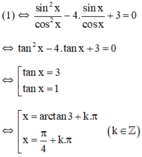
Vậy phương trình có tập nghiệm
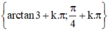 (k ∈ Z)
(k ∈ Z)
Đúng 0
Bình luận (0)
Giải phương trình sau: \(\cot x-1=\dfrac{\cos2x}{1+\tan x}+\sin^2x-\dfrac{1}{2}\sin2x\)
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{cosx}{sinx}-1=\dfrac{cos^2x-sin^2x}{1+\dfrac{sinx}{cosx}}+sin^2x-sinx.cosx\)
\(\Leftrightarrow\dfrac{cosx-sinx}{sinx}=cosx\left(cosx-sinx\right)-sinx\left(cosx-sinx\right)\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(\dfrac{1}{sinx}-cosx+sinx\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(1-sinx.cosx+sin^2x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(3-sin2x-cos2x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(3-\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\right)=0\)
Đúng 0
Bình luận (0)
Giải các PT sau:1. dfrac{left(2cos2x-1right)left(sin x-3right)}{sin x}0 2.dfrac{3left(sin x+cos xright)}{sin x-cos x}2+2cos x3.dfrac{3left(sin x+tan xright)}{tan x-sin x}-2cos x24. 1+sin x+cos x+sin2x+cos2x05. 2sin xleft(1+cos2xright)+sin2x1+2cos x
Đọc tiếp
Giải các PT sau:
1. \(\dfrac{\left(2\cos2x-1\right)\left(\sin x-3\right)}{\sin x}=0\)
2.\(\dfrac{3\left(\sin x+\cos x\right)}{\sin x-\cos x}=2+2\cos x\)
3.\(\dfrac{3\left(\sin x+\tan x\right)}{\tan x-\sin x}-2\cos x=2\)
4. \(1+\sin x+\cos x+\sin2x+\cos2x=0\)
5. \(2\sin x\left(1+\cos2x\right)+\sin2x=1+2\cos x\)
1.
ĐKXĐ: \(x\ne k\pi\)
\(\Leftrightarrow\left(2cos2x-1\right)\left(sinx-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{1}{2}\\sinx=3>1\left(ktm\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
2. Bạn kiểm tra lại đề, pt này về cơ bản ko giải được.
3.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{3\left(sinx+\dfrac{sinx}{cosx}\right)}{\dfrac{sinx}{cosx}-sinx}-2cosx=2\)
\(\Leftrightarrow\dfrac{3\left(1+cosx\right)}{1-cosx}+2\left(1+cosx\right)=0\)
\(\Leftrightarrow\left(1+cosx\right)\left(\dfrac{3}{1-cosx}+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\left(loại\right)\\cosx=\dfrac{5}{2}\left(loại\right)\end{matrix}\right.\)
Vậy pt đã cho vô nghiệm
Đúng 1
Bình luận (1)
4.
\(\Leftrightarrow\left(sin^2x+cos^2x+2sinx.cosx\right)+\left(sinx+cosx\right)+\left(cos^2x-sin^2x\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)^2+\left(sinx+cosx\right)+\left(sinx+cosx\right)\left(cosx-sinx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sinx+cosx+1+cosx-sinx\right)=0\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=0\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{2\pi}{3}+k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình
2
sin
2
x
+
3
sin
2
x
3
Đọc tiếp
Giải phương trình 2 sin 2 x + 3 sin 2 x = 3
![]()
![]()
![]()
![]()
Đáp án B
Sử dụng phương pháp giải phương trình đẳng cấp bậc 2 đối với sin và cos bằng cách chia cả 2 vế phương trình cho cos 2 x
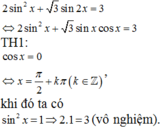

Đúng 0
Bình luận (0)
: Vật dao động cho bởi phương trình: x = sin2 (πt + π/2) − cos2 (πt + π/2) (cm), t đo bằng giây. Hỏi vật có dao động điều hòa không ? Nếu có, tính chu kì dao động. A. không. B. có, T = 0,5 s. C. có, T = l s. D. có, T = 1,5 s.
Giải phương trình
sin
x
+
cos
x
cos
x
-
sin
x
1
+
sin
2
x
A.
x
π
/
4
+
k
π
h...
Đọc tiếp
Giải phương trình sin x + cos x cos x - sin x = 1 + sin 2 x
A. x = π / 4 + k π h o ặ c x = k π
B. x = - π / 4 + k 2 π h o ặ c x = k 2 π
C. x = - π / 4 + k π h o ặ c x = k 2 π
D. x = - π / 4 + k π h o ặ c x = k π
Giải phương trình sau :
\(\cot x-\tan x+4\sin2x=\dfrac{2}{\sin2x}\)
Đối với những phương trình lượng giác chứa \(\tan x,\cot x,\sin2x\) hoặc \(\cos2x\) ta có thể đưa về phương trình chứa \(\cos x,\sin x,\sin2x\) hoặc \(\cos2x\). Ngoài ra ta có thể đặt ẩn phụ \(t=\tan x\) để đưa về phương trình theo t :


Đúng 0
Bình luận (0)
bổ sung cho bạn kia cái đk
đk: sin2x # 0
<=> 2x # kπ
<=> x # kπ/2
4cos^2(2x) - 2cos2x - 2 = 0
tới đây giải tiếp sẽ ra 2 nghiệm là
cos2x = 1 hoặc cos2x = -1/2
nghiệm cos2x = 1 loại vì cos2x = 1 thì sin2x = 0 ( mâu thuẫn với điều kiện ) ai không hiểu thì vẽ cái đường tròn ra là biết ngay
Đúng 0
Bình luận (0)