Tìm số diểm chung của đường thẳng d : x = 12 + 4 t y = 9 + 3 t z = 1 + t và mặt phẳng ( α ) : 3 x + 5 y - z - 2 = 0 .
A. Vô số điểm chung
B. 0 điểm chung
C. 2 điểm chung
D. 1 điểm chung
Những câu hỏi liên quan
a, vẽ đồ thị hàm số y = \(\dfrac{x^2}{2}\) và đường thẳng (d) : y = x + 4 trên cùng một hệ trục toạ độ
b, tìm toạ độ giao diểm P và d bằng phép tính
1. Cho hàm số y = ax + 3 (d)
a/ Xác định a biết (d) đi qua A(1;-1). Vẽ đồ thị với a vừa tìm được..
b/ Xác định a biết đường thẳng (d) song song với đường thẳng y = 2x – 1(d’)
c/ Tìm tọa độ giao diểm của (d) và (d’) với a tìm được ở câu a bằng phép tính
a: Thay x=1 và y=-1 vào (d), ta được:
a+3=-1
hay a=-4
Đúng 0
Bình luận (0)
Cho 30 diểm phân biệt trong đó có a diểm thẳng hàng , cứ qua 2 điểm ta vẽ được 1 đường thẳng . Tìm a biết số đường thẳng tạo thành là 412 đường thẳng
Cho 2006 đường thẳng trong đó bất kì đường thảng nào cũng cắt nhau. Không có đường thẳng nào đồng qui. Tìm số giao diểm của chúng? cách làm
Trong mặt phẳng Oxy, cho 2 đường thẳng (d) và (d') lần lượt là đồ thị của các hàm số bậc nhất y=x+2 và y=\(\sqrt{3}\) x
a) Vẽ (d) và (d'), tìm tọa độ của điểm chung giữa (d) và (d').
b) Tính số đo các góc tạo bởi mỗi đường thẳng (d) và (d') với trục hoành Ox.
c) Tính số đo của góc nhọn tạo bởi (d) và (d').
a: Phương trình hoành độ giao điểm là:
\(x+2=x\sqrt{3}\)
\(\Leftrightarrow x\cdot\left(1-\sqrt{3}\right)=-2\)
\(\Leftrightarrow x=\sqrt{3}+1\)
Thay \(x=\sqrt{3}+1\) vào (d'), ta được:
\(y=\sqrt{3}\left(\sqrt{3}+1\right)=3+\sqrt{3}\)
Đúng 0
Bình luận (0)
Bài 12: Cho (P): \(y=\dfrac{x^2}{4}\)và đường thẳng (d) đi qua điểm I \(\left(\dfrac{3}{2};1\right)\) có hệ số góc là m
1. Vẽ (P) và viết Phương trình (d)
2. Tìm m sao cho (d) tiếp xúc (P)
3. Tìm m sao cho (d) và (P) có hai điểm chung phân biệt
Cho parabol (P): \(y=\frac{-1}{4}x^2\)và đường thẳng (d): y=(m+1)x+m^2+3(m là tham số).Tìm tất cả các giá trị của m để đường thẳng (d) và parabol (P) không có điểm chung
Phương trình hoành độ giao điểm của (P) với (d):
\(\frac{-1}{4}x^2=\left(m+1\right)x+m^2+3\)
\(\Leftrightarrow x^2+4\left(m+1\right)x+4m^2+12=0\)
\(\Delta'=2^2\left(m+1\right)^2-4m^2-12\)
\(=4m^2+8m+4-4m^2-12\)
\(=8m-8\)
(P) và (d) không có điểm chung khi pt hoành độ giao điểm vô nghiệm.
\(\Leftrightarrow\Delta'< 0\Leftrightarrow8m-8< 0\)
\(\Leftrightarrow m< 1\)
Đúng 0
Bình luận (0)
Phương trình hoành độ giao điểm của (p) và (d) là
\(-\frac{1}{4}x^2=\left(m+1\right)x+m^2+3\)<=> \(\frac{1}{4}x^2+\left(m+1\right)x+m^2+3=0\)
\(\left(a=\frac{1}{4},b=m+1,c=m^2+3\right)\)
\(\Delta=b^2-4ac=\left(m+1\right)^2-4\cdot\frac{1}{4}\left(m^2+3\right)\)
\(=m^2+2m+1-m^2-3=2m-2\)
(p) và (d) không có điểm chung <=> \(\Delta< 0\)
<=> \(2m-2< 0\)<=> \(2m< 2\)<=> \(m< 1\)
Vậy với \(m< 1\)thì (p) và (d) không có điểm chung
Đúng 0
Bình luận (0)
Cho hàm số y=\(\frac{1}{4}x^2\)
Tìm m để đường thẳng (d): y=x+m chỉ có 1 điểm chung với (P). Xác định tọa độ của điểm chung này
Cho hàm số (C):
y
x
3
-
6
x
2
+
9
x
và đường thẳng d:
y
2
m
-
m
2
. Tìm số giá trị của tham số thực m để đường thẳn...
Đọc tiếp
Cho hàm số (C): y = x 3 - 6 x 2 + 9 x và đường thẳng d: y = 2 m - m 2 . Tìm số giá trị của tham số thực m để đường thẳng d và đồ thị (C) có hai điểm chung
A. 4
B. 3
C. 2.
D. Vô số
Đáp án C
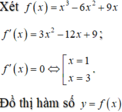
Đồ thị hàm số y = f ( x ) gồm hai phần:
Phần 1. Giữ nguyên phần đồ thị nằm phía trên trục hoành.
Phần 2. Lấy đối xứng phần nằm dưới trục hoành qua trục hoành
Dựa vào đồ thị, ta thấy đường thẳng d và đồ thị (C) có hai điểm chung khi
Đúng 0
Bình luận (0)