Biểu thức sin α + sin 2 α 1 + cos α + cos 2 α bằng
A. - cos α
B. c o t α
C. - tan α
D. tan α
Tìm đẳng thức đúng:
A. tg α = sin α + cos α B. tg α = sin α - cos α
C. tg α = sin α . cos α D. tgα = sin α /cos α
Chứng minh R
sin4α + sin2α . cos2α + cos2α = 1
\(\dfrac{sin\text{α}}{1-cos\text{α}}\)+\(\dfrac{sin\text{α}}{1+cos\text{α}}\)+\(\dfrac{2}{sin\text{α}}\)
\(\dfrac{sin\text{α}}{1+cos\text{α}}\)+\(\dfrac{1+cos\text{α}}{sin\text{α}}\)=\(\dfrac{2}{sin\text{α}}\)
a: VT=sin^2a(sin^2a+cos^2a)+cos^2a
=sin^2a+cos^2a
=1=VP
b: \(VT=\dfrac{sina+sina\cdot cosa+sina-sina\cdot cosa}{1-cos^2a}=\dfrac{2sina}{sin^2a}=\dfrac{2}{sina}=VP\)
c: \(VT=\dfrac{sin^2a+1+2cosa+cos^2a}{sina\left(1+cosa\right)}\)
\(=\dfrac{2\left(cosa+1\right)}{sina\left(1+cosa\right)}=\dfrac{2}{sina}=VP\)
Chứng minh các hệ thức:
a) \(\dfrac{cos\text{ α }}{1-sin\text{ α}}=\dfrac{1+sin\text{ α}}{cos\text{ α}}\)
b)\(\dfrac{\left(sin\text{ α }+cos\text{ α }\right)^2-\left(sin\text{ α }-cos\text{ α }\right)^2}{sin\text{ α }cos\text{ α }}=4\)
a: \(\dfrac{\cos\alpha}{1-\sin\alpha}=\dfrac{1+\sin\alpha}{\cos\alpha}\)
\(\Leftrightarrow\cos^2\alpha=1-\sin^2\alpha\)(đúng)
b: Ta có: \(\dfrac{\left(\sin\alpha+\cos\alpha\right)^2-\left(\sin\alpha-\cos\alpha\right)^2}{\sin\alpha\cdot\cos\alpha}\)
\(=\dfrac{4\cdot\sin\alpha\cdot\cos\alpha}{\sin\alpha\cdot\cos\alpha}\)
=4
bài 1: a)biết sin α=√3/2.tính cos α,tan α,cot α
b)cho tan α=2.tính sin α,cos α,cot α
c)biết sin α=5/13.tính cos,tan,cot α
bài 2
biết sin α x cos α=12/25.tính sin,cos α
1:
a: sin a=căn 3/2
\(cosa=\sqrt{1-sin^2a}=\sqrt{1-\dfrac{3}{4}}=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
\(tana=\dfrac{\sqrt{3}}{2}:\dfrac{1}{2}=\sqrt{3}\)
cot a=1/tan a=1/căn 3
b: \(tana=2\)
=>cot a=1/tan a=1/2
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2a}=5\)
=>cos^2a=1/5
=>cosa=1/căn 5
\(sina=\sqrt{1-cos^2a}=\sqrt{\dfrac{4}{5}}=\dfrac{2}{\sqrt{5}}\)
c: \(cosa=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
tan a=5/13:12/13=5/12
cot a=1:5/12=12/5
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị
của các góc nhọn α.
a) A = cos4α + 2cos2α . sin2α + sin4a
b) B = sin4α + cos2α . sin2α + cos2α
c) C = 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos α
d) D = (tan α - cot α )2 - (tan α + cot α )2
e) E = 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)
f) F = \(\dfrac{1}{1+sin\text{α}}\)+\(\dfrac{1}{1-sin\text{α}}\)-2 tan2α
Cho góc α thỏa mãn tanα = 2. Tính giá trị biểu thức P = 1 + cos α + cos 2 α sin α + sin 2 α
A. P = 4
B. P = 1/2
C. P = 1
D. P = 1/4
Chọn B.
Ta có: 1 + cos2α = 2cos2α và sin2α = 2sinα.cosα.
Mà tanα = 2 nên cot α = 1/2
Suy ra:
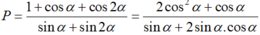
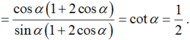
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
rút gọn:
1, 1-sin2α
2, (1+cos α)(1-cos α)
3, 1+sin2α+cos2α
4,sin α-sin α.cos2α
5, sin4α+cos4α+2.sin2α.cos2α
6,tan2α-sin2α.tan2α
7, cos2α+tan2α.cos2α
8, tan2α.(2.cos2α+sin2α-1)
\(1+\sin^2\alpha+\cos^2\alpha=1+1=2\)
Chứng minh : \(\dfrac{sin^2\text{α}}{cos\text{α}\left(1+tan\text{α}\right)}-\dfrac{cos^2\text{α}}{sin\text{α}\left(1+cot\text{α}\right)}-sin\text{α}-cos\text{α}\)
Trong các hệ thức sau, hệ thức nào không đúng ?
(A) (sin α+cos α)^2=1+2sin α cos α;
(B) (sinα−cosα)2=1−2sinαcosα(sinα−cosα)2=1−2sinαcosα;
(C) cos^4α−sin^4α=cos^2α−sin^2α;
(D) cos^4α+sin^4α=1.
Ta có:
(sin α+cos α)^2
=sin^2α + 2sin α cos α + cos^2 α
=1+2sin α cos α
Nên A đúng
(sin α−cos α)^2
=sin^2 α−2sin α cos α+cos^2α
=(sin^2α+cos^2α)−2sin α cos α
=1−2sin α cos α
Nên B đúng
cos^4 α−sin^4 α
=(cos^2 α−sin^2 α)(cos^2 α+sin^2 α)
=(cos^2 α−sin^2 α).1
=cos^2 α−sin^2 α
Nên C đúng
cos^4 α+sin^4 α
=(sin^2 α+cos^2 α )^2−2sin^2 α cos^2 α
=1−2 sin^2 α cos^2 α.
Nên D sai chọn D
ko bít có đúng ko nx
Bạn ơi! Toán từ lớp 10 trở lên bạn vào hoc 24 để gửi câu hỏi nhé!
Bài này câu D sai.
Bạn thay \(\alpha=\frac{\pi}{2}\) vào thử nhé!