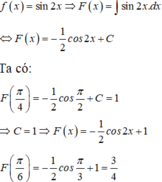Tính nguyên hàm I = ∫ x - 2 sin 3 x d x = - x - a cos 3 x b + 1 c sin 3 x + C
Tính giá trị của tổng S = a + b + c.
Chọn đáp án đúng
A. S = 14
B. S = - 2
C. S = 9
D. S = 10
Tính đạo hàm của các hàm số sau:
a) \(y = x{\sin ^2}x;\)
b) \(y = {\cos ^2}x + \sin 2x;\)
c) \(y = \sin 3x - 3\sin x;\)
d) \(y = \tan x + \cot x.\)
tham khảo:
a)\(y'=xsin2x+sin^2x\)
\(y'=sin^2x+xsin2x\)
b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)
c)\(y=sin3x-3sinx\)
\(y'=3cos3x-3cosx\)
d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)
\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)
Tính tổng tất cả các giá trị nguyên của hàm số y = 3 . sin x - cos x - 4 2 . sin x + cos x - 3
A. 8
B. 5
C. 6
D. 9
Tính nguyên hàm của các hàm sau:
1. \(\int sin^2\)\(\dfrac{x}{2}\) dx
2. \(\int cos^23x\) dx
3. \(\int4cos^2\dfrac{x}{2}\) dx
\(\int sin^2\dfrac{x}{2}dx=\int\left(\dfrac{1}{2}-\dfrac{1}{2}cosx\right)dx=\dfrac{1}{2}x-\dfrac{1}{2}sinx+C\)
\(\int cos^23xdx=\int\left(\dfrac{1}{2}+\dfrac{1}{2}cos6x\right)dx=\dfrac{1}{2}x+\dfrac{1}{12}sin6x+C\)
\(\int4cos^2\dfrac{x}{2}dx=\int\left(2+2cosx\right)dx=2x+2sinx+C\)
Tìm họ nguyên hàm của hàm số lượng giác sau :
\(f\left(x\right)=\int\frac{4\sin x+3\cos x}{\sin x+2\cos x}dx\)
Biến đổi :
\(4\sin x+3\cos x=A\left(\sin x+2\cos x\right)+B\left(\cos x-2\sin x\right)=\left(A-2B\right)\sin x+\left(2A+B\right)\cos x\)
Đồng nhất hệ số hai tử số, ta có :
\(\begin{cases}A-2B=4\\2A+B=3\end{cases}\)\(\Leftrightarrow\begin{cases}A=2\\B=-1\end{cases}\)
Khi đó \(f\left(x\right)=\frac{2\left(\left(\sin x+2\cos x\right)\right)-\left(\left(\sin x-2\cos x\right)\right)}{\left(\sin x+2\cos x\right)}=2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\)
Do đó,
\(F\left(x\right)=\int f\left(x\right)dx=\int\left(2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\right)dx=2\int dx-\int\frac{\left(\cos x-2\sin x\right)dx}{\sin x+2\cos x}=2x-\ln\left|\sin x+2\cos x\right|+C\)
f(x)=4sin2x.cos2x.sinx=4(1-cos2x)cos2x.sinx=(4cos4x-4cos2x)(-sinx)
Đặt u=cosx ---> F(x)=(4/5)cos5x-(4/3)cos3x+C
Xét tính chẵn lẻ của các hàm số sau:
a) \(y = \sin 2x + \tan 2x\); b) \(y = \cos x + {\sin ^2}x\);
c) \(y = \sin x\cos 2x\); d) \(y = \sin x + \cos x\).
a) Hàm số \(y = \sin 2x + \tan 2x\) có nghĩa khi \(tan 2x\) có nghĩa
\(\cos 2x \ne 0\;\; \Leftrightarrow 2x \ne \frac{\pi }{2}\;\;\;\; \Leftrightarrow x \ne \frac{\pi }{4} + \frac{{k\pi }}{2}\) \
Vây tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - 2x} \right) + \tan \left( { - 2x} \right) = - \sin 2x - \tan 2x = - \left( {\sin 2x + \tan 2x} \right) = - f\left( x \right),\;\forall x \in D\).
Vậy \(y = \sin 2x + \tan 2x\) là hàm số lẻ
b) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cos \left( { - x} \right) + {\sin ^2}\left( { - x} \right) = \cos x + {\sin ^2}x = f\left( x \right),\;\forall x \in D\)
Vậy \(y = \cos x + {\sin ^2}x\) là hàm số chẵn
c) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right)\cos \left( { - 2x} \right) = - \sin x.\cos 2x = - f\left( x \right),\;\forall x \in D\)
Vậy \(y = \sin x\cos \;2x\) là hàm số lẻ
d) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) + \cos \left( { - x} \right) = - \sin x + \cos x \ne f\left( x \right),\;\forall x \in D\)
Vậy \(y = \sin x + \cos x\) không là hàm số chẵn cũng không là hàm số lẻ
Tính đạo hàm cấp hai của mỗi hàm số sau:
a) \(y = 2{x^4} - 3{x^3} + 5{x^2}\)
b) \(y = \frac{2}{{3 - x}}\)
c) \(y = \sin 2x\cos x\)
d) \(y = {e^{ - 2x + 3}}\)
e) \(y = \ln (x + 1)\)
f) \(y = \ln ({e^x} + 1)\)
\(a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}\)
\(c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}\)
e,
\(y = \ln (x + 1) \Rightarrow y' = \frac{1}{{x + 1}} \Rightarrow y'' = - \frac{1}{{{{\left( {x + 1} \right)}^2}}}\)
f,
\(y = \ln ({e^x} + 1) \Rightarrow y' = \frac{{{e^x}}}{{{e^x} + 1}} \Rightarrow y'' = - \frac{{{e^x}.{e^x}}}{{{{\left( {{e^x} + 1} \right)}^2}}} = - \frac{{{e^{2x}}}}{{{{\left( {{e^x} + 1} \right)}^2}}}\)
Tính đạo hàm của các hàm số sau:
a) \(y = \sin 3x\);
b) \(y = {\cos ^3}2x\);
c) \(y = {\tan ^2}x\);
d) \(y = \cot \left( {4 - {x^2}} \right)\).
a) Đặt \(u = 3{\rm{x}}\) thì \(y = \sin u\). Ta có: \(u{'_x} = {\left( {3{\rm{x}}} \right)^\prime } = 3\) và \(y{'_u} = {\left( {\sin u} \right)^\prime } = \cos u\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = \cos u.3 = 3\cos 3{\rm{x}}\).
Vậy \(y' = 3\cos 3{\rm{x}}\).
b) Đặt \(u = \cos 2{\rm{x}}\) thì \(y = {u^3}\). Ta có: \(u{'_x} = {\left( {\cos 2{\rm{x}}} \right)^\prime } = - 2\sin 2{\rm{x}}\) và \(y{'_u} = {\left( {{u^3}} \right)^\prime } = 3{u^2}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = 3{u^2}.\left( { - 2\sin 2{\rm{x}}} \right) = 3{\left( {\cos 2{\rm{x}}} \right)^2}.\left( { - 2\sin 2{\rm{x}}} \right) = - 6\sin 2{\rm{x}}{\cos ^2}2{\rm{x}}\).
Vậy \(y' = - 6\sin 2{\rm{x}}{\cos ^2}2{\rm{x}}\).
c) Đặt \(u = \tan {\rm{x}}\) thì \(y = {u^2}\). Ta có: \(u{'_x} = {\left( {\tan {\rm{x}}} \right)^\prime } = \frac{1}{{{{\cos }^2}x}}\) và \(y{'_u} = {\left( {{u^2}} \right)^\prime } = 2u\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = 2u.\frac{1}{{{{\cos }^2}x}} = 2\tan x\left( {{{\tan }^2}x + 1} \right)\).
Vậy \(y' = 2\tan x\left( {{{\tan }^2}x + 1} \right)\).
d) Đặt \(u = 4 - {x^2}\) thì \(y = \cot u\). Ta có: \(u{'_x} = {\left( {4 - {x^2}} \right)^\prime } = - 2{\rm{x}}\) và \(y{'_u} = {\left( {\cot u} \right)^\prime } = - \frac{1}{{{{\sin }^2}u}}\).
Suy ra \(y{'_x} = y{'_u}.u{'_x} = - \frac{1}{{{{\sin }^2}u}}.\left( { - 2{\rm{x}}} \right) = \frac{{2{\rm{x}}}}{{{{\sin }^2}\left( {4 - {x^2}} \right)}}\).
Vậy \(y' = \frac{{2{\rm{x}}}}{{{{\sin }^2}\left( {4 - {x^2}} \right)}}\).
Biết F(x) là một nguyên hàm của hàm f(x) = sin 2x và F π 4 = 1 .Tính F π 6
A. F π 6 = 5 4
B. F π 6 = 0
C. F π 6 = 3 4
D. F π 6 = 1 2
Chọn đáp án C
Vì F(x) là một nguyên hàm của hàm