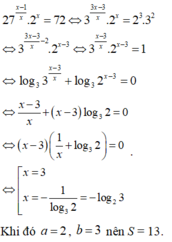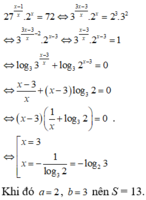Chứng minh rằng số P=4n(a2+b2) luôn viết được dưới dạng m2+n2 với a,b,m,n là các số nguyên dương.

Những câu hỏi liên quan
Cho a= \(\sqrt{2}-1\)
a) Viết a2 , a3 dưới dạng \(\sqrt{m}-\sqrt{m-1}\) trong đó m là số tự nhiên .
b*) Chứng minh rằng với mọi số nguyên dương n, số an viết được dưới dạng trên.
Cho a,b là các số chẵn. Chứng minh rằng a2 + b2 viết được dưới dạng hiệu hai bình phương của 2 số nguyên
Vì a,b là các số chẵn nên a,b viết được dưới dạng là a=2m và b=2n(Với m,n∈Z)
Ta có: \(a^2+b^2\)
\(=\left(2m\right)^2+\left(2n\right)^2\)
\(=4m^2+4n^2\)
\(=4\left(m^2+n^2\right)\)
\(=2\left(2m^2+2n^2\right)\)
\(=\left(m^2+n^2+1-m^2-n^2+1\right)\cdot\left(m^2+n^2+1+m^2+n^2-1\right)\)
\(=\left(m^2+n^2+1\right)^2-\left(m^2+n^2-1\right)^2\)
là bình phương của hai số nguyên(đpcm)
Đúng 0
Bình luận (0)
1.Cho a,b,c là các số nguyên tố thoả mãn: ab + 1 = c. CMR: a2+ c hoặc b2+ c là số chính phương
2.Cho m,n là các số nguyên dương thoả mãn: m2+n2+m⋮mn. CMR: m là một số chính phương
Chứng minh rằng số có dạng (33...3)2, trong đó có n chữ số 3 (với n là số nguyên dương), luôn viết được dưới dạng hiệu của số tự nhiên viết bởi toàn chữ số 1 và số tự nhiên viết bởi toàn chữ số 2.
Toán lớp 6Toán chứng minh
ket ban voi to di anh thu
Chứng minh rằng số có dạng (33...3)2, trong đó có n chữ số 3 (với n là số nguyên dương), luôn viết được dưới dạng hiệu của số tự nhiên viết bởi toàn chữ số 1 và số tự nhiên viết bởi toàn chữ số 2.
Ta có\(33333.....3^2=33333...3\cdot3333....3\)(Mỗi số có n chữ số 3)
=9999...9x1111...1(Mỗi thừa số có n chữ số)
=(10000...01-2)x1111...1(thừa số thứ nhất có n-1 chữ số 0,thừa số thứ hai có n chữ số 1)
=1111....1-2222...2(số bị trừ có 2n chữ số , số trừ có n chữ số)
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh rằng: m2 + n2 = 2(a2 + b2).
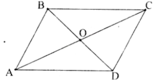
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
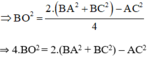
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
Đúng 0
Bình luận (0)
Biết phương trình
27
x
-
1
x
.
2
x
72
có một nghiệm viết dưới dạng
x
-
log
a
b
, với a, b là các số nguyên dương nhỏ hơn 8. Khi đó tính tổng
S
...
Đọc tiếp
Biết phương trình 27 x - 1 x . 2 x = 72 có một nghiệm viết dưới dạng x = - log a b , với a, b là các số nguyên dương nhỏ hơn 8. Khi đó tính tổng S = a 2 + b 2
A. S = 29
B. S = 25
C. S = 13
D. S = 34
Chứng minh rằng số có dạng (333...3)2, trong đó có n chữ số 3 (với n là số nguyên dương), luôn được viết dưới dạng hiệu của số tự nhiên viết bởi toàn chữ số 1 và số tự nhiên viết bởi toàn chữ số 2.
Biết phương trình
27
x
-
1
x
.
2
x
27
có một nghiệm viết dưới dạng
x
-
log
a
b
, với a, b là các số nguyên dương nhỏ hơn 8. Khi đó tính tổng
S
a
2
+
b...
Đọc tiếp
Biết phương trình 27 x - 1 x . 2 x = 27 có một nghiệm viết dưới dạng x = - log a b , với a, b là các số nguyên dương nhỏ hơn 8. Khi đó tính tổng S = a 2 + b 2 .
A. S = 29
B. S = 25
C. S = 13
D. S = 34