Hai đường cong y = x 3 + 5 4 x - 2 C 1 và y = x 2 + x - 2 C 2 tiếp xúc nhau tại điểm M 0 x 0 ; y 0 . Tìm phương trình đường thẳng d là tiếp tuyến chung C 1 và C 2 tại điểm M 0 .
A. y = - 5 4
B. y = 2x - 9 4
C. y = 5 4
D. y = 2x + 9 4
Những câu hỏi liên quan
Bài 1: Viết phương trình đồ thị hàm sốa) yx^3-3x^2+2 tại điểm (-1;-2)b) ydfrac{x^2+4x+5}{x+2} tại điểm có hoành độ bằng 0Bài 2: Viết phương trình tiếp tuyến với:a) Đường cong (C): yx^3+x-3 tại điểm có hoành độ bằng -1b) Đường cong (C): yx^3-3x^2 tại điểm có tung độ bằng -4c) Đường cong (C): ydfrac{x-3}{2x+1} tại điểm có hoành độ bằng -1Bài 3: Viết phương trình tiếp tuyến với:a) Đường cong (C): ydfrac{1}{3}3x^3-2x^2+3x+1 biết tiếp tuyến song song đường thẳng ydfrac{-3}{4}xb) Đường cong (C): ydfr...
Đọc tiếp
Bài 1: Viết phương trình đồ thị hàm số
a) \(y=x^3-3x^2+2 \) tại điểm (-1;-2)
b) \(y=\dfrac{x^2+4x+5}{x+2}\) tại điểm có hoành độ bằng 0
Bài 2: Viết phương trình tiếp tuyến với:
a) Đường cong (C): \(y=x^3+x-3\) tại điểm có hoành độ bằng -1
b) Đường cong (C): \(y=x^3-3x^2\) tại điểm có tung độ bằng -4
c) Đường cong (C): \(y=\dfrac{x-3}{2x+1}\) tại điểm có hoành độ bằng -1
Bài 3: Viết phương trình tiếp tuyến với:
a) Đường cong (C): \(y=\dfrac{1}{3}3x^3-2x^2+3x+1\) biết tiếp tuyến song song đường thẳng \(y=\dfrac{-3}{4}x\)
b) Đường cong (C): \(y=\dfrac{x^2+3x+1}{-x-2}\) biết tiếp tuyến song song với đường thẳng 2x+y-5=0
Bài 4: Cho đường cong (C): \(y=\dfrac{x^2-2x+2}{x-1}\). Viết phương trình tiếp tuyến của (C) biết:
a) Tại điểm có hoành độ bằng 6
b) Song song với đường thẳng \(y=-3x+29\)
c) Vuông góc với đường thẳng \(y=\dfrac{1}{3}x+2\)
Bài 5: Cho hàm số \(y=\dfrac{3x-2}{x-1}\) (C). Viết phương trình tiếp tuyến của đồ thị hàm số (C) biết:
a) Tiếp tuyến đi qua A(2;0)
b) Tiếp tuyến tạo với trục hoành 1 góc 45°
Mình làm xong hết rồi nhưng mà không biết đúng hay không. Nhờ mọi người giải giúp mình để mình thử đối chiếu đáp án được không ạ?
Cho đường cong (C) là đồ thị của hàm số y = x^2 - 4x + 3. Viết pt tiếp tuyến của đường cong đó. a) tại điểm Mo = (-2, 15) b) tại điểm có tung độ x = 3 c) k = 4
\(y'=2x-4\)
a.
\(y'\left(-2\right)=2.\left(-2\right)-4=-8\)
Phương trình tiếp tuyến:
\(y=-8\left(x+2\right)+15\Leftrightarrow y=-8x-1\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm
\(\Rightarrow x_0^2-4x_0+3=3\Rightarrow x_0^2-4x_0=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=0\Rightarrow y'\left(0\right)=-4\\x_0=4\Rightarrow y'\left(4\right)=4\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=-4\left(x-0\right)+3\\y=4\left(x-4\right)+3\end{matrix}\right.\) \(\Leftrightarrow...\)
c.
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow y'\left(x_0\right)=k=4\)
\(\Rightarrow2x_0-4=4\Rightarrow x_0=4\)
\(\Rightarrow y\left(4\right)=3\)
Pttt: \(y=4\left(x-4\right)+3\Leftrightarrow y=4x-13\)
Đúng 0
Bình luận (0)
cho vecto v(-1;2) đường cong C có pt (x-2)^2 + (y-3)^2 = 9 tìm pt của đường cong C' là ảnh của C qua phép tịnh tiến theo v
(C) có \(\left\{{}\begin{matrix}I\left(2;3\right)\\R=3\end{matrix}\right.\)
\(T_{\overrightarrow{v}}\left(I\right)=I'\left(x',y'\right)\)\(\Rightarrow\left\{{}\begin{matrix}x'=x+a=2+\left(-1\right)=1\\y'=y+a=3+2=5\end{matrix}\right.\Rightarrow I'\left(1,5\right)\)
\(T_{\overrightarrow{v}}\left(C\right)=\left(C'\right)\) có \(\left\{{}\begin{matrix}I'\left(1,5\right)\\R=3\end{matrix}\right.\)
\(\Rightarrow\) \(\left(C'\right):\left(x-1\right)^2+\left(y-5\right)^2=3\)
Đúng 1
Bình luận (0)
Cho đường cong (C):
y
x
-
2
x
+
2
. Điểm nào dưới đây là giao của hai tiệm cận của (C)? A. L(-2;1) B. M(2;1) C. N(-2;-2) D. K(-2;2)
Đọc tiếp
Cho đường cong (C): y = x - 2 x + 2 . Điểm nào dưới đây là giao của hai tiệm cận của (C)?
A. L(-2;1)
B. M(2;1)
C. N(-2;-2)
D. K(-2;2)
Đáp án A.
Đồ thị hàm số có tiệm cận ngang y = 1.
Đồ thị hàm số có tiện cận đứng x = -2
Giao điểm của hai tiệm cận là L(-2;1)
Đúng 0
Bình luận (0)
(d):mx-y+m=0 cắt đường cong (C):y=x^3-3x^2+4 tại ba điểm phân biệt lần lượt tại A B và C(-1;0) sao cho tam giác OAB có S=5 căn 5.Khi đó m là
Thể tích khối tròn xoay khi quay xung quanh trục Ox hình phẳng giới hạn bởi đường cong
y
4
-
x
2
, trục hoành và hai đường thẳng x0;x2 là A.
32
3
π
B.
π
2
C. 2
π
2
D.
16
3
π
Đọc tiếp
Thể tích khối tròn xoay khi quay xung quanh trục Ox hình phẳng giới hạn bởi đường cong y = 4 - x 2 , trục hoành và hai đường thẳng x=0;x=2 là
A. 32 3 π
B. π 2
C. 2 π 2
D. 16 3 π
Cho hai hàm số yf(x) và yg(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số yf’(x) là đường cong nét đậm, đồ thị hàm số yg’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của yf’(x) và yg’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)f(x)-g(x) trên đoạn [a;c] A.
m
i
n
h
x...
Đọc tiếp
Cho hai hàm số y=f(x) và y=g(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số y=f’(x) là đường cong nét đậm, đồ thị hàm số y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [a;c]
A. m i n h x a ; c = h 0
B. m i n h x a ; c = h a
C. m i n h x a ; c = h b
D. m i n h x a ; c = h c
Cho hình thang cong (H) giới hạn bởi các đường
y
3
x
,
y
0
,
x
0
,
x
2
. Đường thẳng xt (0t2) chia (H) thành hai phần có diện tích S1 và S2 (như hình vẽ). Tìm t để S13 S2
Đọc tiếp
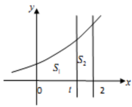
Cho hình thang cong (H) giới hạn bởi các đường y = 3 x , y = 0 , x = 0 , x = 2 . Đường thẳng x=t (0<t<2) chia (H) thành hai phần có diện tích S1 và S2 (như hình vẽ). Tìm t để S1=3 S2
:Cho hai hàm số bậc nhất y ( m - 2 )x +7 và y= (2m -5 )x -8,đô thị của hai hàm số là hai đường thẳng song song khi m bằng : A. -3 B.-4 C.3 D.4
cho đường cong (C) là đồ thị của Hàm Số y = 2x^3 - 2x^2 - 4x + 1. viết phương trình tiếp tuyến của đường cong C tại điểm có hoành độ x=0
\(y'=6x^2-4x-4\)
\(y'\left(0\right)=-4\)
\(y\left(0\right)=1\)
Do đó pt tiếp tuyến tại điểm có hoành độ x=0 là:
\(y=-4\left(x-0\right)+1\Leftrightarrow y=-4x+1\)
Đúng 1
Bình luận (0)