Cho các số thực x, y thỏa mãn x + y = 2 x - 3 + y + 3 . Giá trị nhỏ nhất của biểu thức P = 4 ( x 2 + y 2 ) + 15 x y là:
A. minP = -83
B. minP = -63
C. minP = -80
D. minP = -91
Các số thực x, y thỏa mãn x - 3 3 + i + y - 3 3 - i = i . Khi đó, tổng T = x + y bằng
A. 4
B. 5
C. 6
D. 7
Cho các số thực dương x,y,z thỏa mãn: x2+y2+z2=3. Chứng minh rằng:x3+y3+z3+x+y+z ≥ 6
\(x^3+x\ge2\sqrt{x^4}=2x^2\)
Tương tự:
\(y^3+y\ge2y^2\)
\(z^3+z\ge2z^2\)
Cộng vế:
\(x^3+y^3+z^3+x+y+z\ge2\left(x^2+y^2+z^2\right)=6\)
Dấu "=" xảy ra khi \(x=y=z=1\)
Tìm các số thực x,y,z thỏa mãn (x−1)^2 +|3y−1|+|z+2| = 0.
Ta có: \(\left(x-1\right)^2\ge0\forall x\)
\(\left|3y-1\right|\ge0\forall y\)
\(\left|z+2\right|\ge0\forall z\)
Do đó: \(\left(x-1\right)^2+\left|3y-1\right|+\left|z+2\right|\ge0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left(x,y,z\right)=\left(1;\dfrac{1}{3};-2\right)\)
Tìm các số thực x,y thỏa mãn \(\hept{\begin{cases}x^2+y^2=9\\x^3+y^3=-27\end{cases}}\)
Các số thực x, y thỏa mãn đẳng thức x(3 + 5i) - y(1 + 2i) = 9 + 16i . Giá trị biểu thức T = |x - y| là
A. 0
B. 1
C. 3
D. 5
Chọn D
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
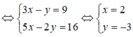
Vậy: T = |x - y| = 5
Cho các số thực dương x,y thỏa mãn xy+x+1 = 3y. Chứng minh rằng x3.y3+1≥2y3
\(xy+x+1=3y\Rightarrow x+\dfrac{1}{y}+\dfrac{x}{y}=3\)
Ta có:
\(x^3+1+1\ge3x\)
\(\dfrac{1}{y^3}+1+1\ge\dfrac{3}{y}\)
\(x^3+\dfrac{1}{y^3}+1\ge\dfrac{3x}{y}\)
Cộng vế:
\(2\left(x^3+\dfrac{1}{y^3}\right)+5\ge3\left(x+\dfrac{1}{y}+\dfrac{x}{y}\right)=9\)
\(\Rightarrow x^3+\dfrac{1}{y^3}\ge2\)
\(\Rightarrow x^3y^3+1\ge2y^3\) (đpcm)
Dấu "=" xảy ra khi \(x=y=1\)
Các số thực x, y thỏa mãn: (x + 2y) + (2x - y)i = 6 + 7i. Giá trị biểu thức T = x + y bằng:
A. 4
B. 5
C. 6
D. 7
Ta có: (x + 2y) + (2x - y)i = 6 + 7i
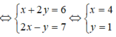
Vậy: T = 4 + 1 = 5
Chọn B
Cho các số thực x,y,z thỏa mãn x^2022+y^2022+z^2022=x^2023+y^2023+z^2023, tính P=x^2021+y^2022+z^2023.
Cho các số thực x,y,z thỏa mãn x+y+z=5 và xy+yz+zx=8. Tìm GTLN,GTNN của x,y,z