Chọn D
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
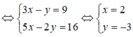
Vậy: T = |x - y| = 5
Chọn D
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
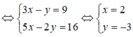
Vậy: T = |x - y| = 5
Các số thực x, y thỏa mãn: (x + 2y) + (2x - y)i = 6 + 7i. Giá trị biểu thức T = x + y bằng:
A. 4
B. 5
C. 6
D. 7
Số phức z = a + bi có phần thực, phần ảo là các số nguyên và thỏa mãn: z 3 = 2 + 11 i . Giá trị biểu thức T = a + b là
A. 2
B. 3
C. 4
D. 5
Xét các số thực dương a, thỏa mãn a+b=1 . Tìm giá trị nhỏ nhất của biểu thức P=a^2 +b
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
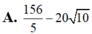
![]()
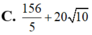
![]()
Cho các số phức z 1 = - 1 + i , z 2 = 1 - 2 i , z 3 = 1 + 2 i . Giá trị của biểu thức T = | z 1 z 2 + z 2 z 3 + z 3 z 1 | là
A. 1
B. 13
C. 5
D. 13
Số phức z thỏa mãn z + 1 z = 3 . Giá trị biểu thức T = z 2006 + 1 z 2006 bằng
A. 1
B. 2
C. 3
D. 3 672
Tìm số phức z thỏa mãn | z - 1 - i | = 5 và biểu thức T = | z - 7 - 9 i | + 2 | z - 8 i | đạt giá trị nhỏ nhất
![]()
![]()
![]()
![]()
Cho các số phức z 1 = - 1 + i , z 2 = 1 - 2 i , z 3 = 1 + 2 i . Giá trị của biểu thức T = z 1 z 2 + z 2 z 3 + z 3 z 1 là
A. 1
B. 3
C. 4
D. 5
Giả sử phương trình l o g 2 2 x - ( m - 2 ) l o g 2 x + 2 m = 0 có hai nghiệm thực phân biệt x 1 , x 2 thỏa mãn x 1 + x 2 = 6 . Giá trị của biểu thức x 1 - x 2 là
A.3
B.8
C.2
D.4