Đơn giản biểu thức C = (1- sin2x) cot2x + 1 - cot2x.
A. sin2x
B. tan2x
C. cot2x
D. cos2x
chứng minh
a> cot2x/1+cot2x . 1+tan2x/tan2x = tan2x+cot2x/1=tan4x
b>tan2x-cos2x/sin2x + cot2x-sin2x/cos2x = 2
a: \(VT=\dfrac{cot^2x}{1+cot^2x}\cdot\dfrac{1+tan^2x}{tan^2x}\)
\(=\dfrac{cot^2x}{\dfrac{1}{sin^2x}}\cdot\dfrac{\dfrac{1}{cos^2x}}{tan^2x}\)
\(=\dfrac{cot^2x}{tan^2x}\cdot\dfrac{1}{cos^2x}:\dfrac{1}{sin^2x}\)
\(=\dfrac{cot^2x}{tan^2x}\cdot\dfrac{sin^2x}{cos^2x}\)
\(=cot^2x\)
\(VP=\dfrac{tan^2x+cot^2x}{1+tan^4x}=\dfrac{\dfrac{sin^2x}{cos^2x}+\dfrac{cos^2x}{sin^2x}}{1+\dfrac{sin^4x}{cos^4x}}\)
\(=\dfrac{sin^4x+cos^4x}{sin^2x\cdot cos^2x}:\dfrac{cos^4x+sin^4x}{cos^4x}\)
\(=\dfrac{sin^4x+cos^4x}{sin^2x\cdot cos^2x}\cdot\dfrac{cos^4x}{cos^4x+sin^4x}=\dfrac{cos^2x}{sin^2x}=cot^2x\)
=>VT=VP
b:
\(\dfrac{tan^2x-cos^2x}{sin^2x}+\dfrac{cot^2x-sin^2x}{cos^2x}\)
\(=\dfrac{\left(\dfrac{sinx}{cosx}\right)^2-cos^2x}{sin^2x}+\dfrac{\left(\dfrac{cosx}{sinx}\right)^2-sin^2x}{cos^2x}\)
\(=\dfrac{sin^2x-cos^4x}{cos^2x\cdot sin^2x}+\dfrac{cos^2x-sin^4x}{sin^2x\cdot cos^2x}\)
\(=\dfrac{sin^2x+cos^2x-cos^4x-sin^4x}{cos^2x\cdot sin^2x}\)
\(=\dfrac{1-\left(cos^2x+sin^2x\right)^2+2\cdot cos^2x\cdot sin^2x}{cos^2x\cdot sin^2x}\)
\(=\dfrac{2\cdot cos^2x\cdot sin^2x}{cos^2x\cdot sin^2x}=2\)
Đơn giản biểu thức A = (1 - sin 2 x ) c o t 2 x + (1 - c o t 2 x ), ta có:
A. A = - cos 2 x
B. A = cos 2 x
C. A = sin 2 x
D. A = - sin 2 x
Đáp án: C
Ta có:
A = (1 - sin 2 x ) c o t 2 x + (1 - c o t 2 x ) = c o t 2 x - sin 2 x . c o t 2 x + 1 - c o t 2 x
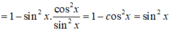
Đơn giản biểu thức A = (1 - sin2x) .cot2x + (1 - cot2x) ta được :
A. sin2x
B. 2
C. 1
D. cot2x
B = tan2 x . (cot2x + cos2x + sin2x – 1 ) + 10
B = sin2 230 + + sin2670 – cos600
Giúp mình với mn...
1)cos2x+cos22x+cos23x+cos24x=2
2) (1-tanx) (1+sin2x)=1+tanx
3) tan2x=sin3x.cosx
4) tanx +cot2x=2cot4x
5) sinx+sin2x+sin3x=cosx+cos2x+cos3x
6)sinx=√2 sin5x-cosx
7) 1/sin2x + 1/cos2x =2/sin4x
8) sinx+cosx=cos2x/1-sin2x
9)1+cos2x/cosx= sin2x/1-cos2x
10)sin3x+cos3x/2cosx-sinx=cos2x
Giải các phương trình :
a) \(\cos3x-\sin2x=0\)
b) \(\tan x\tan2x=-1\)
c) \(\sin3x+\sin5x=0\)
d) \(\cot2x\cot3x=1\)
Á dụng công thức \(cotx-cot2x=\dfrac{1}{sin2x}\) để rút gọn biểu thức sau
\(S=\dfrac{1}{sina}+\dfrac{1}{sin2a}+\dfrac{1}{sin4a}+\dfrac{1}{sin8a}\)
B=\(\dfrac{sin2x}{tanx+cot2x}\)
`B=(sin2x)/(tanx+cot2x)`
Tử ` = 2sinxcosx`
Mẫu `=(sinx)/(cosx) + (cos2x)/(sin2x)`
`=(sinx . sin2x + cosx .cos2x)/(2sinx cosx . cosx)`
`=(cos (2x-x))/(2sinxcos^2x)`
`=(cosx)/(2sinxcos^2x)`
`=1/(2sinxcosx)`
`=> B = sin^2 2x`
Lớp 8 nên không chắc ạ.
\(B=\dfrac{sin2x}{tanx+cot2x}=\dfrac{2sinx.cosx}{\dfrac{sinx}{cosx}+\dfrac{cos2x}{sin2x}}=\dfrac{2sinx.cosx}{\dfrac{sinx.sin2x+cos2x.cosx}{cosx.sin2x}}=\dfrac{2sinx.cosx}{\dfrac{.2sin^2x.cosx+cosx\left(2cos^2x-1\right)}{cosx.2sinx.cosx}}=\dfrac{2sinx.cosx.}{\dfrac{cosx\left(2sin^2x+2cos^2x-1\right)}{cos.2sinx.cosx}}=\dfrac{2sinx.cosx}{\dfrac{1}{2sinx.cosx}}=2sinx.cosx.2sinx.cosx=sin^22x.\)
Giải phương trình sau: 1 + sin 2 x + cos 2 x 1 + cot 2 x = 2 sinx . sin 2 x
A. x = - π 4 + k2π
B. x = - π 4 + k π 2
C. x = π 2 + kπ; π 4 + k2π
D. x = π 2 + kπ