Hệ phương trình 5 x + y = 7 − x − 3 y = 21 nhận cặp số nào sau đây là nghiệm?
A. (1; 2)
B. (8; −3)
C. (3; −8)
D. (3; 8)
Cho hệ phương trình 2 x - 3 y + 4 z = - 5 - 4 x + 5 y - z = 6 3 x + 4 y - 3 z = 7 . Giả sử (x;y;z) là nghiệm của hệ phương trình, khi đó x+y+z bằng
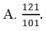
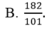
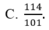
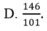
Cho hệ phương trình 2.x+y=5 và m.x-y=-7. tìm m để phương trình có 1 nghiệm duy nhất. Hệ phương trình có thể có vô số nghiệm hay ko
Ta có định lý sau:
Hệ \(\hept{\begin{cases}a_1x+b_1y=c_1\\a_2x+b_2y=c_2\end{cases}}\)
- Có 1 nghiệm duy nhất khi \(\frac{a_1}{a_2}\ne\frac{b_1}{b_2}\)
- Có vô số nghiệm khi \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Do đó \(\hept{\begin{cases}2x+y=5\\mx-y=-7\end{cases}}\) có 1 nghiệm duy nhất \(\Leftrightarrow\) \(\frac{2}{m}\ne\frac{1}{-1}\) \(\Leftrightarrow\) \(m\ne-2\)
Hệ pt ko thể có vô số nghiệm vì \(\frac{1}{-1}\ne\frac{5}{-7}\)
Giải các hệ phương trình sau:
{ (x - 5)(y - 2) = (x + 2)(y - 1)
{ (x - 4)(y + 7) = (x - 3)(y + 4)
\(\left\{{}\begin{matrix}\left(x-5\right)\left(y-2\right)=\left(x+2\right)\left(y-1\right)\\\left(x-4\right)\left(y+7\right)=\left(x-3\right)\left(y+4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy-2x-5y+10=xy-x+2y-2\\xy+7x-4y-28=xy+4x-3y-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+7y=12\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+21y=36\\3x-y=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}22y=20\\x+7y=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{62}{11}\\y=\dfrac{10}{11}\end{matrix}\right.\)
cho hệ phương trình x + y = 3k - 2
2x - y = 5 với k là tham số
giải hệ phương trình khi k = 1
tìm k để hệ phương trình có nghiệm ( x ; y) sao cho x^2 - y - 5/ y + 1 = 4
Thay k=1 và HPT ta có:
\(\left\{{}\begin{matrix}x+y=3.1-2\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x+y=1\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+2y=2\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+2y=2\\3y=-3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)
Vậy HPT có nghiệm (x;y) = (2;-1)
b) tìm k để hệ phương trình có nghiệm ( x ; y) sao cho \(x^2-y-\dfrac{5}{y}+1=4\)
\(\left\{{}\begin{matrix}x+y=3k-2\\2x-y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\2x-\left(3k-2-x\right)=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\2x-3k+2+x=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\3x=3k+3\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=3k-2-x\\x=k+1\end{matrix}\right.\)
Ta có \(\text{ x= k+1 }=>y=2k-3\) (*)
Thay vào biểu thức đã cho ở đề bài ta có :
\(x^2-y-\dfrac{5}{y}+1=4\)
⇔\(\left(k+1\right)^2-2k+3-\dfrac{5}{2k-3}+1=4\)
⇔\(k^2+2k+1-2k+3-\dfrac{5}{2k-3}+1=4\)
Sau một hồi bấm máy tính Casio thì ra k=2
Vậy k=2 thì Thỏa mãn yêu cầu đề bài
Lần sau bạn dùng Latex đánh đề bài cho dễ nhìn nha, mình sợ chép lại đề bài bị sai @@
giải hệ phương trình 4x-y=-5 và 2|y-2x| + |x+y-1|=7
giải hệ phương trình
\(\left\{{}\begin{matrix}xy+x+y=5\\xy+x^2+y^2=7\end{matrix}\right.\)
đặt x+y = u ; xy = v đk: u2 ≥ 4v
\(\left\{{}\begin{matrix}u+v=5\\u^2-v=7\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}u^2+u-12=0\left(1\right)\\u+v=5\left(2\right)\end{matrix}\right.\)
từ pt 1 => \(\left[{}\begin{matrix}u=-4\\u=3\end{matrix}\right.\)
nghiệm u = - 4 loại
u = 3 nhận => v = 2
<=> x+y = 3 ; xy = 2
đặt x+y = S ; xy = P đk: S2 ≥ 4P
=> x và y là nghiệm của phương trình
X2 - SX + P = 0
= X2 - 3X + 2 = 0
=> \(\left[{}\begin{matrix}X=2\\X=1\end{matrix}\right.\)
vậy (x;y) = {(1;2);(2;1)}
cho hệ phương trình\(\hept{\begin{cases}3x-my=-9\\mx+2y=16\end{cases}}\)
a) giải hệ phương trình khi m = 5
b) chứng tỏ rằng hệ phương trình luôn luôn có nghiệm duy nhất với mọi m
c) định m để hệ có nghiệm (x ; y) = (1,4 ; 6,6)
d) với trị nguyên nào của m để hệ có nghiệm (x ; y) thỏa mãn x + y = 7
giúp mình với mình cần nộp trong ngày 17/2/2020
Giải mấy bài này mệt ghê ~
a,Thay m = 5 vào PT \(\hept{\begin{cases}3x-my=-9\\mx+2y=16\end{cases}}\)
\(< =>\hept{\begin{cases}3x-5y=-9\\5x+2y=16\end{cases}}\)
\(< =>\hept{\begin{cases}15x-25y=-45\\15x+6y=48\end{cases}}\)
\(< =>\hept{\begin{cases}31y=93\\3x-5y=-9\end{cases}}\)
\(< =>\hept{\begin{cases}y=3\\3x=6\end{cases}}\)
\(< =>\hept{\begin{cases}y=3\\x=2\end{cases}}\)
b,Ta thay : \(\hept{\begin{cases}y=3\\x=2\end{cases}}\)vào PT ta đc :
\(\hept{\begin{cases}6-3m=-9\\2m+6=16\end{cases}}\)
\(< =>\hept{\begin{cases}m=5\\m=5\end{cases}}\)(đề sai ? hay do mk ngu ?)
c,bạn thay nghiệm vào là đc nhé <3
Cho hệ phương trình: 2X +Y = 3m-2 ( m là tham số ) X - Y = 5 a) Giải hệ phương trình khi m = - 4 ; b) Tìm m để hệ phương trình có nghiệm (x; y) thỏa mãn: x + y = 13.
Giải các hệ phương trình x - 3 y + 2 x = - 7 - 2 x + 4 y + 3 z = 8 3 x + y - z = 5
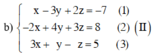
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (1) với (3) rồi trừ đi phương trình (3) ta được:
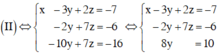
Giải hệ phương trình trên ta được 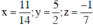
Vậy hệ phương trình có nghiệm 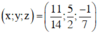
Giải các phương trình và hệ phương trình sau :
1. \(3x^2-7x+2=0\)
2. \(x^4-5x+4=0\)
3. \(\left\{{}\begin{matrix}\sqrt{5}x-2y=7\\x-\sqrt{5}y=2\sqrt{5}\end{matrix}\right.\)
1. 3x( x - 2 ) - ( x - 2 ) = 0
<=> ( x-2).(3x-1) = 0 => x = 2 hoặc x = \(\dfrac{1}{3}\)
2. x( x-1 ) ( x2 + x + 1 ) - 4( x - 1 )
<=> ( x - 1 ).( x (x^2 + x + 1 ) - 4 ) = 0
(phần này tui giải được x = 1 thôi còn bên kia giải ko ra nha )
3 \(\left\{{}\begin{matrix}\sqrt{5}x-2y=7\\\sqrt{5}x-5y=10\end{matrix}\right.\)<=> \(\left\{{}\begin{matrix}y=-1\\x=\sqrt{5}\end{matrix}\right.\)
\(1. 3x^2 - 7x +2=0\)
=>\(Δ=(-7)^2 - 4.3.2\)
\(= 49-24 = 25\)
Vì 25>0 suy ra phương trình có 2 nghiệm phân biệt:
\(x_1\)=\(\dfrac{-\left(-7\right)+\sqrt{25}}{2.3}=\dfrac{7+5}{6}=2\)
\(x_2\)=\(\dfrac{-\left(-7\right)-\sqrt{25}}{2.3}=\dfrac{7-5}{6}=\dfrac{1}{3}\)