Cho ∫ 0 1 x d x ( 2 x + 1 ) 2 = a + b ln 2 + c ln 3 với a, b, c là các số hữu tỉ. Giá trị của a+b+c bằng:
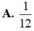
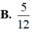
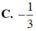
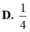
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
a, Cho `0<x<25`
Tìm GTLN:`(80-2x)(50-2x)x`
b, `0<x<2`. Tìm GTLN: `5x(2-x)`
c, `x≥2`. Tìm GTLN: `x + 1/x`
d, Cho `x,y>0, x+y≤1`. TÌm GTNN: `x + y + 1/x + 1/y`
d. Áp dụng BĐT Caushy Schwartz ta có:
\(x+y+\dfrac{1}{x}+\dfrac{1}{y}\le x+y+\dfrac{\left(1+1\right)^2}{x+y}=x+y+\dfrac{4}{x+y}\le1+\dfrac{4}{1}=5\)
-Dấu bằng xảy ra \(\Leftrightarrow x=y=\dfrac{1}{2}\)
c. Bạn kiểm tra lại đề nhé.
b. \(5x\left(2-x\right)=-5x\left(x-2\right)=-5\left(x^2-2x\right)=-5\left(x^2-2x+1-1\right)=-5\left(x-1\right)^2+5\le5\)-Dấu bằng xảy ra \(\Leftrightarrow x=1\)
a.
\(\left(80-2x\right)\left(50-2x\right)x=\dfrac{2}{3}\left(40-x\right)\left(50-2x\right)3x\le\dfrac{2}{3}\left(\dfrac{40-x+50-2x+3x}{3}\right)^3=18000\)
Dấu "=" xảy ra khi \(40-x=50-2x=3x\Leftrightarrow x=10\)
b.
\(5x\left(2-x\right)=5.x\left(2-x\right)\le\dfrac{5}{4}\left(x+2-x\right)^2=5\)
Dấu "=" xảy ra khi \(x=2-x\Rightarrow x=1\)
c.
Biểu thức này chỉ có min, ko có max
d.
\(x+y\le1\Rightarrow-\left(x+y\right)\ge-1\)
\(x+y+\dfrac{1}{x}+\dfrac{1}{y}=\left(4x+\dfrac{1}{x}\right)+\left(4y+\dfrac{1}{y}\right)-3\left(x+y\right)\ge2\sqrt{\dfrac{4x}{x}}+2\sqrt{\dfrac{4y}{y}}-3.1=5\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
Cho mk hỏi:
câu 1: Chứng minh đẳng thức:
-a.(c-d)-d.(a+c))=-c.(a+d)
Câu 2: Tìm X
1/x.(x+7)=0
2/(x+12).(x-3)=0
3/(-x+5).(3-x)=0
4/x.(2+x).(7-x)=0
5/(x-1).(x+2).(-x-3)=0
Câu 1 : \(-a.\left(c-d\right)-d.\left(a+c\right)=-c.\left(a+d\right)\)
Ta có : \(VT=-a.\left(c-d\right)-d\left(a+c\right)\)
\(=-ac+ad-da-dc\)
\(=-ac-dc\)
\(=-c\left(a+d\right)=VP\)
\(\Rightarrow-a\left(c-d\right)-d\left(a+c\right)=-c\left(a+d\right)\left(đpcm\right)\)
Câu 2 :
1, \(x.\left(x+7\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x+7=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x=-7\end{cases}}}\)
2, \(\left(x+12\right)\left(x-3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x+12=0\\x-3=0\end{cases}\Rightarrow\orbr{\begin{cases}x=-12\\x=3\end{cases}}}\)
3, \(\left(-x+5\right)\left(3-x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}-x+5=0\\3-x=0\end{cases}\Rightarrow\orbr{\begin{cases}x=5\\x=3\end{cases}}}\)
4, \(x\left(2+x\right)\left(7-x\right)=0\)
\(\Rightarrow x=0;2+x=0\)hoặc \(7-x=0\)
\(\Rightarrow x=0;x=-2\)hoặc \(x=7\)
Cho biểu thức f(x) = (-x + 1)(x - 2). Khẳng định nào sau đây đúng: A. f(x) < 0, ∀x ∈ (1; +∞) B. f(x) < 0, ∀x ∈ (-∞; 2) C. f(x) > 0, ∀x ∈ R D. f(x) > 0, ∀x ∈ (1; 2)
a) C = ( x - 1).( x - 2).( 3 - x). Tìm x sao cho C < 0
b) D = ( x^2 - 4). ( 16 - x^2 ). Tìm x sao cho D > hoặc = 0
cái này dùng bảng xét dấu là nhanh nhất. mình làm mẫu cho một cái, bạn xem rồi tự tìm hiểu nha. nếu vẫn k hiểu thì liên hệ mình giải nốt cho. bảng xét dấu này lấy nghiệm của từng nhân tử rồi theo quy tắc phải cùng, trái khác để xét dấu
D= (x-2)(x+2).(4-x)(4+x)
a) C<0
nhìn bảng xét dấu ta có thể thấy rằng tích này âm trong 2 trường hợp: \(1\le x\le2\)và x>3
tương tự làm với câu 2 nha
a) C = ( x - 1).( x - 2).( 3 - x). Tìm x sao cho C < 0
b) D = ( x^2 - 4). ( 16 - x^2 ). Tìm x sao cho D > hoặc = 0
a) C < 0 <=>
hoặc x - 1 < 0 => x < 1
hoặc x - 2 < 0 => x < 2
hoặc x - 3 < 0 => x < 3
Vậy x < 3 thỏa mãn đề bài.
Mn giúp mk vs:
Tìm x, bt:
a.(x-2)(x+3)>0
b.(x-2)(x-1)>0
c.(x-2)(x^2+1)>0
d.(x-1)(x+2)>0
Tìm x,y thỏa mãn:
a.x(y+3)=3
b.(x-1)(y+2)=-3
c.x+3chia hết cho x+1
d.2x+3 chia hết cho x+1
a.x(y+3)=3
=> x(y+3) ∈Ư(3)={-3;-1;1;3}
ta có bảng sau
| x | -3 | -1 | 1 | 3 |
| y+3 | -1 | -3 | 3 | 1 |
| y | -4 | -6 | 0 | -2 |
vậy x=-3 thì y=-4
x=-1 thì y=-6
x=1 thì y=0
x=3 thì y=-2
c.x+3⋮ x+1
=> (x+3)-(x+1)⋮(x+1)
=> (x+3-x-1)⋮(x+1)
=> 2⋮(x+1)
=> (x+1) ∈ Ư(2)={-2;-1;1;2}
=> x∈{-3;-2;0;1}
vậy x ∈{-3;-2;0;1}
b,d tương tự
a.(x-2)(x+3)>0
=>\(\left[{}\begin{matrix}x-2>0\\x+3>0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x>2\\x>-3\end{matrix}\right.\)
=> x>2
vậy x>2
b.(x-2)(x-1)>0
=> \(\left[{}\begin{matrix}x-2>0\\x-1>0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x>2\\x>1\end{matrix}\right.\)
=> x>2
vậy x>2
c.(x-2)(x2+1)>0
=> \(\left[{}\begin{matrix}x-2>0\\x^2+1>0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x>2\\x^2>-1\Rightarrow x>\sqrt{-1}\end{matrix}\right.\)
vậy x>2
d.(x-1)(x+2)>0
=> \(\left[{}\begin{matrix}x-1>0\\x+2>0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x>1\\x>-2\end{matrix}\right.\)
=> x>1
vậy x>1
Còn câu này nx bn ạ:
x^2.(x+2)<0
Tìm x
Giúp mk nhanh nha, mk cần gấp
1, Cho D = ( x2 -2 ) .( 16- x2)
Tìm x để D >0 hoặc D= 0
Bài 1 giải các pt sau và diễn tập nghiệm trên trục số a) 2x-6>0 b) -3x+9>0 c)3(x-1)+5>(x+1)+3 d)x/3 - 1/2>x/6 Bài 2:a)cho a>b chứng minh 3a+7>3b+7 b)cho a >b chứng minh a+3>b+1 c) cho 5a -1>5b-1 hãy so sánh a và b Bài 3: 2x(x+5)=0 b) X^2-4=0 d) (x-5)(2x+1)+(x-5)(x+6)=0 Ở bài 1 câu a có dấu hoặc bằng nữa nha bài 2 câu c cũng vậy
3:
a: =>x=0 hoặc x+5=0
=>x=0 hoặc x=-5
b: =>x^2=4
=>x=2 hoặc x=-2
c: =>(x-5)(2x+1+x+6)=0
=>(x-5)(3x+7)=0
=>x=5 hoặc x=-7/3
1.
a. 2x - 6 > 0
\(\Leftrightarrow\) 2x > 6
\(\Leftrightarrow\) x > 3
S = \(\left\{x\uparrow x>3\right\}\)
b. -3x + 9 > 0
\(\Leftrightarrow\) - 3x > - 9
\(\Leftrightarrow\) x < 3
S = \(\left\{x\uparrow x< 3\right\}\)
c. 3(x - 1) + 5 > (x - 1) + 3
\(\Leftrightarrow\) 3x - 3 + 5 > x - 1 + 3
\(\Leftrightarrow\) 3x - 3 + 5 - x + 1 - 3 > 0
\(\Leftrightarrow\) 2x > 0
\(\Leftrightarrow\) x > 0
S = \(\left\{x\uparrow x>0\right\}\)
d. \(\dfrac{x}{3}-\dfrac{1}{2}>\dfrac{x}{6}\)
\(\Leftrightarrow\dfrac{2x}{6}-\dfrac{3}{6}>\dfrac{x}{6}\)
\(\Leftrightarrow2x-3>x\)
\(\Leftrightarrow2x-3-x>0\)
\(\Leftrightarrow x-3>0\)
\(\Leftrightarrow x>3\)
\(S=\left\{x\uparrow x>3\right\}\)
2.
a.
Ta có: a > b
3a > 3b (nhân cả 2 vế cho 3)
3a + 7 > 3b + 7 (cộng cả 2 vế cho 7)
b. Ta có: a > b
a > b (nhân cả 2 vế cho 1)
a + 3 > b + 3 (cộng cả 2 vế cho 3) (1)
Ta có; 3 > 1
b + 3 > b + 1 (nhân cả 2 vế cho 1b) (2)
Từ (1) và (2) \(\Rightarrow\) a + 3 > b + 1
c.
5a - 1 + 1 > 5b - 1 + 1 (cộng cả 2 vế cho 1)
5a . \(\dfrac{1}{5}\) > 5b . \(\dfrac{1}{5}\) (nhân cả 2 vế cho \(\dfrac{1}{5}\) )
a > b
3.
a. 2x(x + 5) = 0
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\x+5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(S=\left\{0,-5\right\}\)
b. x2 - 4 = 0
\(\Leftrightarrow x\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(S=\left\{0,4\right\}\)
d. (x - 5)(2x + 1) + (x - 5)(x + 6) = 0
\(\Leftrightarrow\left(x-5\right)\left(2x+1+x+6\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(3x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\3x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{-7}{3}\end{matrix}\right.\)
\(S=\left\{5,\dfrac{-7}{3}\right\}\)
1) cho \(x>0\). CMR: \(x+\dfrac{1}{x}\ge2\)
2) cho a, b, c, d>0. thỏa mãn \(a.b.c.d=1\). CM:
a) \(ab+cd\ge2\)
b) \(a^2+b^2+c^2+d^2\ge4\)
giúp mk vs ạ mk cần gấp
1) Với x > 0 ta có:
\(x+\dfrac{1}{x}\ge2\\ \Leftrightarrow\dfrac{x^2+1}{x}\ge\dfrac{2x}{x}\\ \Leftrightarrow x^2+1\ge2x\left(\text{vì }x>0\right)\\ \Leftrightarrow x^2-2x+1\ge0\\ \Leftrightarrow\left(x-1\right)^2\ge0\left(\text{luôn đúng }\forall x>0\right)\)
Dấu "=" xảy ra \(\Leftrightarrow x=1\). Vậy BĐT được chứng mình với x > 0.
1: Áp dụng Bđt cosi, ta được:
\(x+\dfrac{1}{x}\ge2\cdot\sqrt{x\cdot\dfrac{1}{x}}=2\)
2a)
Có \(abcd=1\Rightarrow ab=\dfrac{1}{cd}\)
Áp dụng BĐT vừa chứng mình ở bài 1, ta có:
\(cd+\dfrac{1}{cd}\ge2\Leftrightarrow ab+cd\ge2\)
Dấu "=" xảy ra \(\Leftrightarrow cd=1\)
Vậy BĐT được chứng minh với a,b,c,d > 0 thỏa mãn abcd = 1.