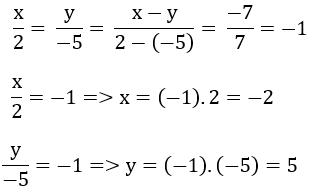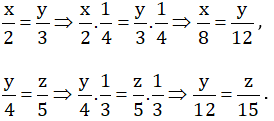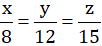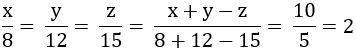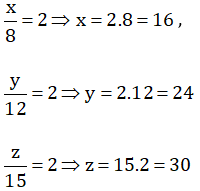Tìm 2 số x và y biết \(x^2+y^2;x^2-y^2;x^2.y^2\)tỉ lệ nghịch với 1/25; 1/7; 1/576 (x;y khác 0)

Những câu hỏi liên quan
1 Tìm 2 số x và y biết x 3 y 2 và 2x 5y 122 Tìm 2 số x và y biết x y 4 5 và x y 133 Tìm 2 số x và y biết 4x 7y và x y 12
1)Tìm 2 số x và y biết x/3=y/-2 và 2x+5y=-12
2) Tìm 2 số x và y biết x:y=4:5 và x-y =13
3) Tìm 2 số x và y biết 4x=7y và x-y=12
a, Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{-2}=\frac{2x+5y}{2.3+5.\left(-2\right)}=-\frac{12}{-4}=3\)
\(x=-3;y=6\)
b, Theo bài ra ta có : \(x:y=4:5\Leftrightarrow\frac{x}{4}=\frac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{5}=\frac{x-y}{4-5}=\frac{13}{-1}=-13\)
\(x=-52;y=-65\)
c, Theo bài ra ta có: \(4x=7y\Leftrightarrow\frac{x}{7}=\frac{y}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{7}=\frac{y}{4}=\frac{x-y}{7-4}=\frac{12}{3}=4\)
\(x=28;y=16\)
a) Tìm 2 số x và y cho biết: dfrac{x}{3}dfrac{y}{4} và x + y 28
b) Tìm 2 số x và y biết x : 2 y : (-5) và x - y (-7)
c) Tìm 3 số x, y, z biết rằng: dfrac{x}{2}dfrac{y}{3} , dfrac{y}{4}dfrac{z}{5} và x + y - z 10
GIÚP MÌNH VỚI Ạ! TKS 3
Đọc tiếp
a) Tìm 2 số x và y cho biết: \(\dfrac{x}{3}\)=\(\dfrac{y}{4}\) và x + y = 28
b) Tìm 2 số x và y biết x : 2 = y : (-5) và x - y = (-7)
c) Tìm 3 số x, y, z biết rằng: \(\dfrac{x}{2}\)=\(\dfrac{y}{3}\) , \(\dfrac{y}{4}\)=\(\dfrac{z}{5}\) và x + y - z = 10
GIÚP MÌNH VỚI Ạ! TKS <3
a) Áp dụng tính chất dãy tỉ số bằng nhau ta được:
X/3 = y/4 = x/3 + y/4 = 28/7 = 4
=> x = 4 × 3 = 12
=> y = 4 × 4 = 16
Vậy x = 12, y = 16
B) Áp dụng tính chất dãy tỉ số bằng nhau ta được:
X/2 = y/(-5) = x/2 - y/(-5) = (-7)/7 = -1
=> x = -1 × 2 = -2
=> y = -1 × -5 = 5
Vậy x = -2, y = 5
C) làm tương tự như bài a, b
Đúng 3
Bình luận (0)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
Đúng 0
Bình luận (0)
1. Tìm 2 số x và y, biết x/2 = y/5 và x + y = -21
2. Tìm 2 số x và y, biết 7x = 3y và x - y = 16
Giải:
1. Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{-21}{7}=-3\)
+) \(\frac{x}{2}=-3\Rightarrow x=-6\)
+) \(\frac{y}{5}=-3\Rightarrow y=-15\)
Vậy x = -6
y = -15
2. Ta có:
\(7x=3y\Rightarrow\frac{7x}{21}=\frac{3y}{21}=\frac{x}{3}=\frac{y}{7}\)
Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{7}=\frac{x-y}{3-7}=\frac{16}{-4}=-4\)
+) \(\frac{x}{3}=-4\Rightarrow x=-12\)
+) \(\frac{y}{7}=-4\Rightarrow y=-28\)
Vậy x = -12
y = -28
Đúng 0
Bình luận (0)
1/ \(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=-\frac{21}{7}=-3\)
\(\frac{x}{2}=-3\Rightarrow x=-6\)
\(\frac{x}{5}=-3\Rightarrow x=-15\)
2/ \(7x=3y\Rightarrow\frac{x}{7}=\frac{y}{3}\)
\(\frac{x}{7}=\frac{y}{3}=\frac{x-y}{7-3}=\frac{16}{4}=4\)
\(\frac{x}{7}=4\Rightarrow x=28\)
\(\frac{y}{3}=4\Rightarrow y=12\)
Đúng 0
Bình luận (0)
Câu 1:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\Rightarrow\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{-21}{7}=-3\)
\(\Rightarrow\begin{cases}\frac{x}{2}=-3\\\frac{y}{5}=-3\end{cases}\)\(\Rightarrow\begin{cases}x=-6\\y=-15\end{cases}\)
Vậy x=-6;y=-15
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a)Tìm 2 số x và y biết x phần 3=y phần 4 và x+y=28
b)Tìm 2 số x và y biết x/2=y/(-5) và x-y=-7
c)(x - 1 phần 5) mũ 2004 +(y+0.4)mũ 100+(2-3)mũ 678 =0
1.
Tìm 2 số x và y biết: \(\frac{x}{2}=\frac{y}{5}\) và x + y = -21
2.
Tìm 2 số x và y biết: 7x = 3y và x - y = 16
ÁP dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{7}=\frac{-21}{7}=-3\)
\(\Leftrightarrow\frac{x}{2}=-3\Leftrightarrow x=-6\)
\(\Leftrightarrow\frac{y}{5}=-3\Leftrightarrow y=-15\)
câu b tương tự
Đúng 0
Bình luận (0)
\(\frac{x}{2}=\frac{y}{5}\)
áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{-21}{7}=-3\)
\(\Rightarrow\hept{\begin{cases}x=-3\cdot2=-6\\y=-3\cdot5=-15\end{cases}}\)
vậy___
Đúng 0
Bình luận (0)
a) tìm hai số x và y biết x:2 = y: (-5) và x-y =-7
b) tìm ba số x,y,z biết x phần 2 = y phần 3 ,y phần 4 và z phần 5 và x+y-z=10
cảm ơn trước ak
a) Ta có: \(x:2=y:\left(-5\right)\)
nên \(\dfrac{x}{2}=\dfrac{y}{-5}\)
mà x-y=-7
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-1\\\dfrac{y}{-5}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)
Vậy: (x,y)=(-2;5)
b) Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}\)
nên \(\dfrac{x}{8}=\dfrac{y}{12}\)(1)
Ta có: \(\dfrac{y}{4}=\dfrac{z}{5}\)
nên \(\dfrac{y}{12}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
mà x+y-z=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{8}=2\\\dfrac{y}{12}=2\\\dfrac{z}{15}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\)
Vậy: (x,y,z)=(16;24;30)
Đúng 2
Bình luận (0)
b)
Do đó ta có
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Đúng 0
Bình luận (0)
Bài 1: Tìm hai số x và y, biết x/2 = y/5 và x+ y= -21
Bài 2: Tìm hai số x và y, biết 7x = 3y và x-y = 16
\(\frac{x}{2}=\frac{y}{5}\)và x + y = -21
\(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{-21}{7}=-3\)
\(\Rightarrow\)\(\frac{x}{2}=-3\Rightarrow x=-3.2=-6\)
\(\frac{y}{5}=-3\Rightarrow y=-3.5=-15\)
Bài 2 lập 1 đẳng thức trong 4 đẳng thức đã học rồi làm tương tự như trên nhé
Đúng 0
Bình luận (0)
1, 2, 7x = 3y => x/3 = y/7 mà x - y = 16
ta có x/2 = y/5 mà x + y = -21 => 16/-4 = -4
=> -21/7 = -3 x = -4 x 3 = -12 ; y = -4 x 7 = -28
x = -3 x 2 = -6
y= -3 x 5 = -15
Đúng 0
Bình luận (0)
B1 : x/2 =y/5 và x+y = -21
Áp dụng tính chất dãy tỷ số bằng nhau ta có :
x/2 = y/ 5 = x+y/2+5 = -21/7 = -3
=> x/2 = -3
=> x = -6
=> y/5 = -3
=. y = -15
thử lại xem đúng ko nha bn .
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1.Tìm x,y,z: a.x/5 = -12/20 ; b.2/y = 11/-66 ; c.-3/6 = x/-2 = -18/y = -z/24
Bài 2.Tìm các số nguyên x và y biết : x<0<y và:
-2/x = y/3
Bài 3.Tìm các số nguyên x và y biết x - y = 4 và:
x-3/y-2 = 3/2
Bài 4.Viết dạng chung của tất cả các phân số bằng phân số 21/28
bài 1 : tìm các số x, y , z , t biết : x/2 y/3 ; 7x 2t ; z/t 5/7 và y+ 2z + 3t 10z bài 2 : tìm các số x , y biết a , x:y 4:7 và x +y 44 b, x/2 y/5 và x + y 28 bài 3 : cho M x + 2y - 3z / x - 2y + 3z . tính giá trị của M biết x ,y , z tỉ lệ với 5 ; 4 ; 3 bài 4 : cho a/b c/d . chứng minh a+3b/b c+3d/d ( các tỉ số đều có nghĩa ) làm nhanh cho mình 4 bài này với cảm ơn các friends nhi...
Đọc tiếp
bài 1 : tìm các số x, y , z , t biết :
x/2 = y/3 ; 7x = 2t ; z/t = 5/7 và y+ 2z + 3t = 10z
bài 2 : tìm các số x , y biết a , x:y = 4:7 và x +y = 44
b, x/2 = y/5 và x + y = 28
bài 3 : cho M = x + 2y - 3z / x - 2y + 3z . tính giá trị của M biết x ,y , z tỉ lệ với 5 ; 4 ; 3
bài 4 : cho a/b = c/d . chứng minh a+3b/b = c+3d/d
( các tỉ số đều có nghĩa )
làm nhanh cho mình 4 bài này với
cảm ơn các friends nhiều
Bài 4:
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(a=b\cdot k;c=d\cdot k\)
\(\dfrac{a+3b}{b}=\dfrac{bk+3b}{b}=\dfrac{b\left(k+3\right)}{b}=k+3\)
\(\dfrac{c+3d}{d}=\dfrac{dk+3d}{d}=\dfrac{d\left(k+3\right)}{d}=k+3\)
Do đó: \(\dfrac{a+3b}{b}=\dfrac{c+3d}{d}\)
Bài 2:
a: x:y=4:7
=>\(\dfrac{x}{4}=\dfrac{y}{7}\)
mà x+y=44
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x+y}{4+7}=\dfrac{44}{11}=4\)
=>\(x=4\cdot4=16;y=4\cdot7=28\)
b: \(\dfrac{x}{2}=\dfrac{y}{5}\)
mà x+y=28
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{28}{7}=4\)
=>\(x=4\cdot2=8;y=4\cdot5=20\)
Bài 3:
Đặt \(\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{z}{3}=k\)
=>x=5k; y=4k; z=3k
\(M=\dfrac{x+2y-3z}{x-2y+3z}\)
\(=\dfrac{5k+2\cdot4k-3\cdot3k}{5k-2\cdot4k+3\cdot3k}\)
\(=\dfrac{5+8-9}{5-8+9}=\dfrac{4}{6}=\dfrac{2}{3}\)
Đúng 1
Bình luận (1)