Giá trị của đa thức x + x3 + x5 + x7 + x9 + ...... + x101 tại x = -1 là:
(A) -101;
(B) -100;
(C) -51;
(D) -50
Hãy chọn phương án đúng.
Câu 12. Giá trị của đa thức
x + x3 + x5 + x7 + ... + x101 tại x = -1 là
A. -101. B.
-100 . C.
-51 . D.
-50 .
Câu 13. Trong các biểu thức sau, biểu thức nào không là đơn thức?
A. y4 z6 . B.
-2y4z . C. (yz)10 . D.
-2(y + z) .
Câu 14. Đa thức 6y3 + 6x + 4 - 8x + 5 + 9y3 được thu gọn thành
A. 15y3 + 14x + 9 . B. -3y6 - 2x2 + 9 . C. 15y3 - 2x + 9 . D. 15y3 - 2x -1 .
Câu 15. Đơn thức
- 7 y3x có hệ số và phần biến là:
![]() 2
2
![]() A. - 7
A. - 7
2
và y3x . B. 7 2
và -y3x . C. - 7 2
và -y3x . D. 7 2
và y3x .
![]()
![]()
![]() Câu 16. Thu gọn và tìm bậc của đa thức -y2 + 4y + 8 - 6y - 6y2 -1:
Câu 16. Thu gọn và tìm bậc của đa thức -y2 + 4y + 8 - 6y - 6y2 -1:
A. -7y2 +10y + 7 , bậc 3 . B. -7y2 - 2y + 7 , bậc 2 .
C. 5y4 - 2y2 + 7 , bậc 4 . D. -7y2 - 2y - 9 , bậc 2 .
Câu 17. Đa thức (9x3 - 5x - 5) - (4x2 - 5x + 4)
thu gọn là
A. 9x3 - 4x2 -10x - 9 . B. 9x3 - 4x2 - 9 .
C. 9x3 + 4x2 - 9 . D. 9x3 - 4x2 -1.
Câu 12. Giá trị của đa thức
x + x3 + x5 + x7 + ... + x101 tại x = -1 là
A. -101. B.
-100 . C.
-51 . D.
-50 .
Câu 13. Trong các biểu thức sau, biểu thức nào không là đơn thức?
A. y4 z6 . B.
-2y4z . C. (yz)10 . D.
-2(y + z) .
Câu 14. Đa thức 6y3 + 6x + 4 - 8x + 5 + 9y3 được thu gọn thành
A. 15y3 + 14x + 9 . B. -3y6 - 2x2 + 9 . C. 15y3 - 2x + 9 . D. 15y3 - 2x -1 .
Câu 15. Đơn thức
- 7 y3x có hệ số và phần biến là:
2
A. - 7
2
và y3x . B. 7 2
và -y3x . C. - 7 2
và -y3x . D. 7 2
và y3x .
Câu 16. Thu gọn và tìm bậc của đa thức -y2 + 4y + 8 - 6y - 6y2 -1:
A. -7y2 +10y + 7 , bậc 3 . B. -7y2 - 2y + 7 , bậc 2 .
C. 5y4 - 2y2 + 7 , bậc 4 . D. -7y2 - 2y - 9 , bậc 2 .
Câu 17. Đa thức (9x3 - 5x - 5) - (4x2 - 5x + 4)
thu gọn là
A. 9x3 - 4x2 -10x - 9 . B. 9x3 - 4x2 - 9 .
C. 9x3 + 4x2 - 9 .
bài 4 : phân tích đa thức thành nhân tử rồi tính giá trị của các biểu thức sau :
a, A= 4(x - 2) (x+1) + (2x - 4)2 +(x+1)2 tại x = \(\dfrac{1}{2}\)
b, B= x9 - x7 - x6 - x5 + x4 + x3 + x2 - 1 tại x=1
a,
\(A=4(x-2)(x+1)+(2x-4)^2+(x+1)^2\\=[2(x-2)]^2+2\cdot2(x-2)(x+1)+(x+1)^2\\=[2(x-2)+(x+1)]^2\\=(2x-4+x+1)^2\\=(3x-3)^2\)
Thay $x=\dfrac12$ vào $A$, ta được:
\(A=\Bigg(3\cdot\dfrac12-3\Bigg)^2=\Bigg(\dfrac{-3}{2}\Bigg)^2=\dfrac94\)
Vậy $A=\dfrac94$ khi $x=\dfrac12$.
b,
\(B=x^9-x^7-x^6-x^5+x^4+x^3+x^2-1\\=(x^9-1)-(x^7-x^4)-(x^6-x^3)-(x^5-x^2)\\=[(x^3)^3-1]-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1)-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1-x^4-x^3-x^2)\\=(x^3-1)(x^6-x^4-x^2+1)\)
Thay $x=1$ vào $B$, ta được:
\(B=(1^3-1)(1^6-1^4-1^2+1)=0\)
Vậy $B=0$ khi $x=1$.
$Toru$
Giá trị của đa thức x + x 3 + x 5 + . . . + x 99 tại x = -1 là
A. -100
B. -101
C. -51
D. -50
Tại x = -1 , thay vào đa thức ta được
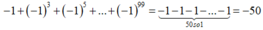
Chọn đáp án D
X x3;X x5;X x7;...X x101=31200
Cho f(x) = 1 + x3 + x5 + x7 + ... + x101. Tính f( 1) ; f( -1)
Thay x = 1 vào f(x) ta được
f(1)=1+13+15+17+…+1101
=1+1+1+…+1 =51.1 =51
Thay x = -1 vào f(x) ta được
f(−1)=1+(−1)3+(−1)5+(−1)7+…+(−1)101
=1+(−1)+(−1)+…+(−1)
=1+50.(−1)=1−50=−49
f(1)=1+13+15+17+…+1101
=1+1+1+…+1 =51.1 =51
Thay x = -1 vào f(x) ta được
f(−1)=1+(−1)3+(−1)5+(−1)7+…+(−1)101
=1+(−1)+(−1)+…+(−1)
=1+50.(−1)=1−50=−49
Cho f ( x ) = 1 + x 3 + x 5 + x 7 + . . . . + x 101 . Tính f(1); f(-1)
A. f(1) = 101; f(-1) = -100
B. f(1) = 51; f(-1) = -49
C. f(1) = 50; f(-1) = -50
D. f(1) = 101; f(-1) = 100
Thay x = 1 vào f(x) ta được
f ( 1 ) = 1 + 1 3 + 1 5 + 1 7 + … + 1 101 = 1 + 1 + 1 + … + 1 ⏟ 51501 = 51.1 = 51
Thay x = -1 vào f(x) ta được
f ( − 1 ) = 1 + ( − 1 ) 3 + ( − 1 ) 5 + ( − 1 ) 7 + … + ( − 1 ) 101 = 1 + ( − 1 ) + ( − 1 ) + … + ( − 1 ) ⏟ 50 : 0 ( − 1 ) = 1 + 50. ( − 1 ) = 1 − 50 = − 49 Vây f ( 1 ) = 51 ; f ( − 1 ) = − 49
Chọn đáp án B
Câu 5.(1,0 điểm):
Cho f(x) = 1 + x3 + x5 + x7 + ... + x101.
Tính f( 1) ; f( -1)
Xác định CTHH của các chất X1, X2, X3, X5, X6, X7, X8, X9 phù hợp để thỏa mãn sơ đồ phản ứng sau. Viết PTHH và ghi gõ điều kiện phản ứng:
X1 + O2 --> X2+X3
X4 + O2 --> X2
X2 --> O2 + X5
X2 + X6 --> Cu + X3
Fe2O3 + X5 --> X3 +X7
X7 + O2 --> X8
X8 + X5 --> X3 + X7
X7 + HCl --> X5 + X9
X8 + X5 --> X3 + X7
X7 + HCl --> X5 + X9
Cho biểu thức sau :
B=[(x4−x+x−3x3+1).(x3−2x2+2x−1)(x+1)x9+x7−3x2−3+1−2(x+6)x2+1].4x2+4x+1(x+3)(4−x)[(x4−x+x−3x3+1).(x3−2x2+2x−1)(x+1)x9+x7−3x2−3+1−2(x+6)x2+1].4x2+4x+1(x+3)(4−x)a, Tìm giá trị của x để giá trị của biểu thức B được xác định
b, Rút gọn B
c, Cmr với các giá trị của x mà giá trị của biểu thức xác định thì −5≤B≤0