Thu gọn đa thức sau:
Q = x2 + y2 + z2 + x2 – y2 + z2 + x2 + y2 – z2
Thu gọn đa thức
C= x2-y2+z2-x2+y2-z2+x2+y2+z2
`@` `\text {Ans}`
`\downarrow`
\(C= x^2-y^2+z^2-x^2+y^2-z^2+x^2+y^2+z^2\)
`= (x^2 - x^2 + x^2) + (-y^2 + y^2 + y^2) + (z^2 - z^2 + x^2)`
`= x^2 + y^2 + z^2`
\(C=x^2-y^2+z^2-x^2+y^2-z^2+x^2+y^2+z^2\)
\(C=\left(x^2-x^2+x^2\right)-\left(y^2-y^2-y^2\right)+\left(z^2-z^2+z^2\right)\)
\(C=x^2-\left(-y^2\right)+z^2\)
\(C=x^2+y^2+z^2\)
Tính tổng của hai đa thức sau: x2 + y2 + z2 và x2 – y2 + z2
(x2 + y2 + z2) + (x2 – y2 + z2)
= x2 + y2 + z2 + x2 – y2 + z2
= (x2 + x2) + (y2 – y2) + (z2 + z2)
= 2x2 + 2z2
phân tích đa thức sau thành nhân tử
e,x(y2-z2)+y(z2-x2)+(z2-y2)....help
phân tích đa thức thành nhân tử
[ (x2 + y2)(z2 + t2) + 4xyzt ]2 - [ 2xy(z2 + t2) + 2zt(x2 + y2) ]
Phân tích các đa thức sau thành nhân tử: x 2 y + x y 2 + x 2 z + x z 2 + y 2 z + y z 2 + 3xyz.
x 2 y + x y 2 + x 2 z + x z 2 + y 2 z + y z 2 + 3xyz.
= ( x 2 y + x 2 z + xyz) + (x y 2 + y 2 z + xyz) + (x z 2 + y z 2 + xyz)
= x(xy + xz + yz) + y(xy + yz + xz) + z(xz + yz + xy)
= (x + y + z)(xy + xz + yz).
\(x^2y+xy^2+x^2z+xz^2+y^2z+yz^2+3xyz\)
\(=\left(x^2y+x^2z+xyz\right)+\left(xz^2+yz^2+xyz\right)+\left(xy^2+y^2z+xyz\right)\)
\(=x\left(xy+xz+yz\right)+z\left(xz+yz+xy\right)+y\left(xy+yz+xz\right)\)
\(=\left(x+y+z\right)\left(xy+yz+xz\right)\)
Cho x, y, z ≠0 và (y2+z2−x2)/2yz +(z2+x2−y2)/2xz +(x2+y2−z2)/2xy =1. Chứng minh rằng trong ba phân thức đã cho có một phân thức bằng 1 và một phân thức bằng -1.
Quy đồng mẫu thức ba phân thức
x x 2 - 2 x y + y 2 - z 2 ; y y 2 - 2 z y + z 2 - x 2 ; z z 2 - 2 z x + x 2 - y 2
x 2 - 2 x y + y 2 - z 2 = x - y 2 - z 2 = (x – y + z)(x – y − z)
y 2 - 2 y z + z 2 - x 2 = y - z 2 - x 2 = (y – z + x)(y – z − x) = -(x +y – z)(x – y + z)
z 2 - 2 z x + x 2 - y 2 = z - x 2 - y 2 = (z – x + y)(z – x -y) = (x- y –z).(x + y – z)
MTC = (x – y + z)(x + y − z)(x – y − z)
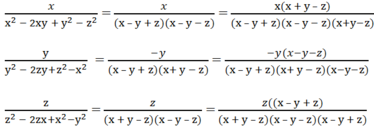
Phân tích đa thức thành nhân tử:
A= x.(y2 - z2) + y.(z2 - x2) + z.(x2 - y2).
B= a.(b3 - c3) + b.(c3 - a3) + c.(a3 - b3).
C= ab.(a + b) - bc.(b + c) + ac. (a - c).
\(A=x\left(y^2-z^2\right)+y\left(z^2-x^2\right)+z\left(x^2-y^2\right)=x\left(y^2-z^2\right)+y\left(-y^2+z^2-x^2+y^2\right)+z\left(x^2-y^2\right)=\left(y^2-z^2\right)\left(x-y\right)+\left(x^2-y^2\right)\left(z-y\right)=\left(y-z\right)\left(y+z\right)\left(x-y\right)-\left(x-y\right)\left(x+y\right)\left(y-z\right)=\left(x-y\right)\left(y-z\right)\left(y+z-x-y\right)=\left(x-y\right)\left(y-z\right)\left(z-x\right)\)
\(B=a\left(b^3-c^3\right)+b\left(c^3-a^3\right)+c\left(a^3-b^3\right)=ab^3-ac^3+bc^3-a^3b+a^3c-b^3c=ab\left(b^2-a^2\right)-c^3\left(a-b\right)+c\left(a^3-b^3\right)=-ab\left(a-b\right)\left(a+b\right)-c^3\left(a-b\right)+c\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)\left(-a^2b-ab^2-c^3+a^2c+abc+b^2c\right)\)
\(C=ab\left(a+b\right)-bc\left(b+c\right)+ac\left(a-c\right)=ab\left(a+b\right)-bc\left(a+b-a+c\right)+ac\left(a-c\right)=ab\left(a+b\right)-bc\left(a+b\right)+bc\left(a-c\right)+ac\left(a-c\right)=b\left(a+b\right)\left(a-c\right)+c\left(a-c\right)\left(a+b\right)=\left(a+b\right)\left(c+c\right)\left(a-c\right)\)
Phan tích đa thức thành nhân tử
1. (b-c)3+(c-a)3+(a-b)3
2. x3+y3+z3-3xyz
3. (x+y)5-x5-y5
4. (x2+y2)3+(z2-x2)3-(y2+z2)3
5. x3-5x2y-14xy2
1. Ta có: hằng đẳng thức: \(x^3+y^3+z^3=3xyz\) nếu x+y+z=0
đặt b-c=x, c-a=y, a-b=z⇒x+y+z=0
\(\Rightarrow\left(b-c\right)^3+\left(c-a\right)^3+\left(a-b\right)^3=3\left(a-b\right)\left(c-a\right)\left(b-c\right)\)
2. \(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)+3xyz-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\)
3. Tham khảo: https://hoc247.net/hoi-dap/toan-8/phan-tich-da-thuc-x-y-5-x-5-y-5-thanh-nhan-tu-faq447273.html
\(5,=x^3+2x^2y-7x^2y-14xy^2\\ =x^2\left(x+2y\right)-7xy\left(x+2y\right)\\ =x\left(x-7y\right)\left(x+2y\right)\)