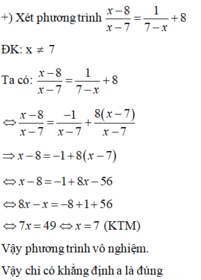Tập nghiệm của phương trình 3 x − 7 x − 1 = 0 là

Những câu hỏi liên quan
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+30 và ( a+1)x-a+202/ Bất phương trình: 5x/5 - 13/21 + x/15 9/25- 2x/35 có nghiệm là....3/ Bất phương trình: 5x-1 2x/5 + 3 có nghiệm là...4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) (4x/3x-x^2) có nghiệm nguyên lớn nhất là...5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 2x -166/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 12 - 2x/37/ Bất phương trình: 2(x-1) - x 3(x-1) - 2x-5 có t...
Đọc tiếp
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Xem thêm câu trả lời
Cho các mệnh sau(I) 5 là nghiệm của phương trình 2x – 3
x
+
2
x
-
4
(II) Tập nghiệm của phương trình 7 – x 2x – 8 là x 5(III) Tập nghiệm của phương trình 10 – 2x 0 là S {5}.Số mệnh đề đúng là: A. 1 B. 0 C. 2 D. 3
Đọc tiếp
Cho các mệnh sau
(I) 5 là nghiệm của phương trình 2x – 3 = x + 2 x - 4
(II) Tập nghiệm của phương trình 7 – x = 2x – 8 là x = 5
(III) Tập nghiệm của phương trình 10 – 2x = 0 là S = {5}.
Số mệnh đề đúng là:
A. 1
B. 0
C. 2
D. 3
+) Thay x = 5 vào phương trình 2 x − 3 = x + 2 x − 4 ta được
2.5 − 3 = 5 + 2 5 − 4 ⇔ 7 = 7 1 = 7
Vậy 5 là nghiệm của phương trình 2 x − 3 = x + 2 x − 4 khẳng định (I) đúng.
+) Tập nghiệm của phương trình 7 – x = 2x – 8 là x = 5 là khẳng định sai vì kết luận x = 5 không phải là tập nghiệm.
+) Ta có: 10 - 2x = 0 ⇔ 2x = 10 ⇔ x = 5
Vậy tập nghiệm của phương trình là S = {5}.
Do đó khẳng định (III) là đúng.
Vậy có hai mệnh đề đúng.
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Trong các khẳng định sau, số khẳng định đúng là:a) Tập nghiệm của phương trình
x
2
+
3
x
x
0
là {0; 3}b) Tập nghiệm của phương trình
x
2
-
4
x
-
2...
Đọc tiếp
Trong các khẳng định sau, số khẳng định đúng là:
a) Tập nghiệm của phương trình x 2 + 3 x x = 0 là {0; 3}
b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0 là {-2}
c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8 là {0}
A. 1
B. 2
C. 0
D. 3
1.Phương trình 2x – 1 = 2x – 1 có số nghiệm là:
2.Phương trình 3x – 2 = x + 4 có nghiệm là:
3.Tập nghiệm của phương trình 2x – 7 = 5 – 4x là:
Phương trình sqrt{2-fleft(xright)}fleft(xright) có tập nghiệm A {1;2;3}. Phương trình sqrt{2.gleft(xright)-1}+sqrt[3]{3.gleft(xright)-2}2.gleft(xright) có tập nghiệm là B {0;3;4;5} . Hỏi tập nghiệm của phương trình sqrt{fleft(xright)-1}+sqrt{gleft(xright)-1}+fleft(xright).gleft(xright)+1fleft(xright)+gleft(xright)
có bao nhiêu phần tử?
A.1
B.4
C.6
D.7
Đọc tiếp
Phương trình \(\sqrt{2-f\left(x\right)}=f\left(x\right)\) có tập nghiệm A = {1;2;3}. Phương trình \(\sqrt{2.g\left(x\right)-1}+\sqrt[3]{3.g\left(x\right)-2}=2.g\left(x\right)\) có tập nghiệm là B = {0;3;4;5} . Hỏi tập nghiệm của phương trình \(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)+1=f\left(x\right)+g\left(x\right)\)
có bao nhiêu phần tử?
A.1
B.4 C.6 D.7
\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)
\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)
\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)
\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)
\(\Leftrightarrow VT\le2g\left(x\right)\)
Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)
\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)
Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)
Ta có:
\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)
\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)
Vậy tập nghiệm của pt đã cho có đúng 1 phần tử
Đúng 0
Bình luận (0)
Viết tập nghiệm của phương trình (x+5)(x-3)=0 và (x+7)(3x-3)
(x+5)(x-3)=0
=>x+5=0 hoặc x-3=0
=>x=-5 hoặc x=3
(x+7)(3x-3)=0
=>x+7=0 hoặc 3x-3=0
=>x=-7 hoặc x=1
Đúng 1
Bình luận (0)
tập nghiệm của phương trình là ∛(x+1) + ∛(7-x) = 2 là?
Lời giải:
Đặt $\sqrt[3]{x+1}=a; \sqrt[3]{7-x}=b$ thì ta có:
$a+b=2$
$a^3+b^3=8$
$\Leftrightarrow (a+b)^3-3ab(a+b)=8$
$\Leftrightarrow 8-6ab=8$
$\Leftrightarrow ab=0$
$\Leftrightarrow a=0$ hoặc $b=0$
Nếu $a=0\Leftrightarrow \sqrt[3]{x+1}=0\Leftrightarrow x=-1$ (thử lại thấy tm)
Nếu $b=0\Leftrightarrow \sqrt[3]{7-x}=0\Leftrightarrow x=7$ (thử lại thấy tm)
Đúng 0
Bình luận (0)
Gọi E là tập nghiệm của phương trình \({x^2} - 2x - 3 = 0\).
G là tập nghiệm của phương trình \((x + 1)(2x - 3) = 0\)
Tìm \(P = E \cap G\).
Ta có:
\({x^2} - 2x - 3 = 0 \Leftrightarrow (x + 1)(x - 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right. \Rightarrow E = \{ - 1;3\} \)
Lại có: \((x + 1)(2x - 3) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \frac{3}{2}\end{array} \right.\)
\( \Rightarrow G = \left\{ { - 1;\frac{3}{2}} \right\}\)
\( \Rightarrow P = E \cap G = \left\{ { - 1} \right\}\).
Đúng 0
Bình luận (0)
Xét phương trình \(x^2-2x-3=0\) có: \(a-b+c=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{c}{a}=3\end{matrix}\right.\Rightarrow E=\left\{-1;3\right\}.\)
Xét phương trình \(\left(x+1\right)\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\Rightarrow G=\left\{-1;\dfrac{3}{2}\right\}.\)
\(\Rightarrow P=E\cap G=\left\{-1\right\}.\)
Đúng 0
Bình luận (0)
Tập nghiệm của phương trình - |5x – 3| = x + 7 là
A. Ø
B. {5/2; 2/3}
C. {5/2; -3/2}
D. {5/2; -2/3}
Tập nghiệm của phương trình |5x – 3| = x + 7 là
A. {5/2}
B. {5/2;2/3}
C. {5/2;-3/2}
D. {5/2; -2/3}