Cho tan α = - 4 5 v ớ i 3 π 2 < α < 2 π . Khi đó :
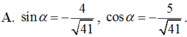
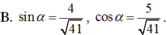
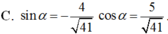
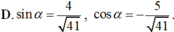
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Cho 2tanα-cotα=1. Tính P=\(\dfrac{\text{tan ( 8 π − α ) + 2 cot ( π + α )}}{3\tan\left(\dfrac{3\pi}{2}+\alpha\right)}\)
2tan a-cot a=1
=>2tana-1/tan a=1
=>\(\dfrac{2tan^2a-1}{tana}=1\)
=>2tan^2a-tana-1=0
=>(tan a-1)(2tana+1)=0
=>tan a=-1/2 hoặc tan a=1
\(P=\dfrac{tan\left(-a\right)+2\cdot cota}{3\cdot tan\left(\dfrac{pi}{2}+a\right)}=\dfrac{-tana+2\cdot cota}{-3\cdot cota}\)
TH1: tan a=-1/2
\(P=\dfrac{\dfrac{1}{2}+2\cdot\left(-2\right)}{-3\cdot\left(-2\right)}=-\dfrac{7}{2}:6=-\dfrac{7}{12}\)
TH2: tan a=1
=>cot a=1
\(P=\dfrac{-1+2}{-3}=\dfrac{1}{-3}=-\dfrac{1}{3}\)
Ta có :
\(2tan\alpha-cot\alpha=1\)
\(\Leftrightarrow2tan\alpha-\dfrac{1}{tan\alpha}=1\)
\(\Leftrightarrow2tan\alpha-\dfrac{1}{tan\alpha}-1=0\)
\(\Leftrightarrow\dfrac{2tan^2\alpha-tan\alpha-1}{tan\alpha}=0\left(tan\alpha\ne0\right)\)
\(\Leftrightarrow2tan^2\alpha-tan\alpha-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tan\alpha=1\\tan\alpha=-\dfrac{1}{2}\end{matrix}\right.\)
\(P=\dfrac{tan\left(8\pi-\alpha\right)+2cot\left(\pi+\alpha\right)}{3tan\left(\dfrac{3\pi}{2}+\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{tan\left(4.2\pi-\alpha\right)+2cot\alpha}{3tan\left(2\pi-\dfrac{\pi}{2}+\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{tan\left(-\alpha\right)+2cot\alpha}{3tan\left[-\left(\dfrac{\pi}{2}-\alpha\right)\right]}\)
\(\Leftrightarrow P=\dfrac{-tan\alpha+2cot\alpha}{-3tan\left(\dfrac{\pi}{2}-\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{-tan\alpha+2cot\alpha}{-3cot\alpha}\)
- Với \(tan\alpha=1\Rightarrow cot\alpha=1\)
\(\Leftrightarrow P=\dfrac{-1+2.1}{-3.1}=-\dfrac{1}{3}\)
- Với \(tan\alpha=-\dfrac{1}{2}\Rightarrow cot\alpha=-2\)
\(\Leftrightarrow P=\dfrac{\dfrac{1}{2}+2.\left(-2\right)}{-3.\left(-2\right)}=\dfrac{-\dfrac{7}{2}}{6}=-\dfrac{7}{12}\)
Cho α ∈ (0;\(\dfrac{\Pi}{2}\)) và tan α = 3. Khi đó sin(α +π) bằng
do a ∈ \(\left(0;\dfrac{\pi}{2}\right)\)⇒ \(\left\{{}\begin{matrix}sinx>0\\cosx>0\end{matrix}\right.\)
Mà tanx = 3 ⇒ \(\dfrac{sinx}{cosx}=3\Leftrightarrow\dfrac{sin^2x}{cos^2x}=9\Rightarrow10sin^2x=9\)
⇒ sinx = \(\dfrac{3}{\sqrt{10}}\)
⇒ sin (x + π) = -sinx = -\(\dfrac{3}{\sqrt{10}}\)
Cho góc α thỏa mãn π 2 < α < π và tan α – cotα = 1. Tính P = tanα + cotα
A. P = 1
B. P = -1
C. P = - 5
D. P = 5
Chọn C.
Ta có tan α – cotα = 1

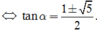
Do ![]() suy ra tanα < 0 nên
suy ra tanα < 0 nên
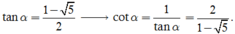
Thay
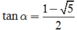 và
và 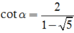
vào P ta được
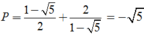
Cho góc α thỏa mãn sin α = 3 5 v à π 2 < α < π .Tính P = tan α 1 + tan 2 α
A. P = 9 25
B. P = 3 25
C. P = 14 25
D. P = - 12 25
Chọn D.
Ta có 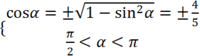 suy ra :
suy ra : ![]()
Thay ![]() vào P ta được
vào P ta được ![]()
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
Đặt điện áp u = U 0 cos(100 π t - π /3)(V) vào hai đầu một tụ điện có điện dung 2. 10 - 4 / π (F). Ớ thời điểm điện áp giữa hai đầu tụ điện là 150 V thìncường độ dòng điện trong mạch là 4 A. Tìm biểu thức của cường độ dòng điện trong mạch.
Theo bài ra ta có
u = U 0 cos(100 π t - π /3)
i = I 0 cos(100 π t - π /3 + π /2) = = I 0 sin(100 π t - π /3)
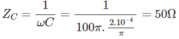
I 0 = U 0 / Z C = U 0 /50
Từ U 0 cos(100 π t - π /3) = 150
⇒ cos(100 π t - π /3) = 150/ U 0
I 0 sin(100 π t - π /3) = 4
⇒ sin(100 π t - π /3) = 200/ U 0
Từ
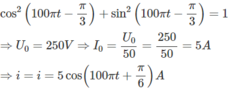
Biểu thức tan(3π/2−α)+cot(3π−α)−cos(π/2−α)+2sin(π+α) sau khi thu gọn là gì?
Online chờ gấp, đa tạ các vị!
\(tan\left(\dfrac{3\pi}{2}-\alpha\right)+cot\left(3\pi-\alpha\right)-cos\left(\dfrac{\pi}{2}-\alpha\right)+2.sin\left(\pi+\alpha\right)\)
\(=tan\left(\pi+\dfrac{\pi}{2}-\alpha\right)+cot\left(-\alpha\right)-sin\alpha+2\left(sin\pi.cos\alpha+cos\pi.sin\alpha\right)\)
\(=tan\left(\dfrac{\pi}{2}-\alpha\right)-cot\alpha-sin\alpha+2.-sin\alpha\)
\(=cot\alpha-cot\alpha-3sin\alpha\)
\(=-3sin\alpha\)
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau tan(3π/2 - α)
cho sinx α =\(\dfrac{-4}{5}\) và π<α<\(\dfrac{\Pi}{2}\) thì sinx α bằng bao nhiêu?
\(sin^2\alpha=1-sin^2\alpha=1-\left(\dfrac{-4}{5}\right)^2=\dfrac{9}{25}\)
vì π<α<\(\dfrac{3\Pi}{2}\)⇒cos α =\(\dfrac{-3}{5}\)
cos2a =1- sin2a =1-\(\left(\dfrac{-4}{5}\right)^2\)=\(\dfrac{3}{5}\)
Vì π<a<\(\dfrac{3\pi}{2}\)
=>cos a =\(\dfrac{-3}{5}\)