Chọn C.
Ta có tan α – cotα = 1

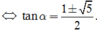
Do ![]() suy ra tanα < 0 nên
suy ra tanα < 0 nên
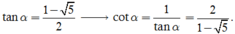
Thay
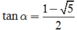 và
và 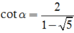
vào P ta được
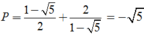
Chọn C.
Ta có tan α – cotα = 1

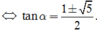
Do ![]() suy ra tanα < 0 nên
suy ra tanα < 0 nên
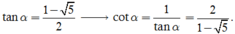
Thay
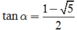 và
và 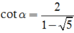
vào P ta được
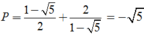
Cho cos α=-2/5 và π<α<3π/2. tính tanα, sinα ,cotα
Cho góc α thỏa mãn tanα + cotα = 5.Tính P = tan3α + cot3α
A. 98
B. 110
C. 112
D. 114
Tính các giá trị lượng giác của góc α, biết
cotα = 4tanα khi π/2 < α < π
Cho 0 < α < π/2. Biểu thức S = sin 4 α - 2 sin 2 α sin 4 α + 2 sin 2 α có thể rút gọn thành biểu thức nào sau đây?
A. - tan 2 α B. tanα
C. c o t 2 α D. cotα
Cho góc α thỏa mãn cos α = - 5 3 và π < α < 3 π 2 .Tính tanα.
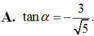
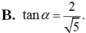
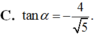
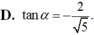
Cho góc α thỏa mãn cos α = - 12 13 và π 2 < α < π .Tính tanα.
![]()
![]()
![]()
![]()
Chứng minh rằng với mọi α, ta luôn có
tan(α + π/2) = -cotα
Nêu định nghĩa của tanα , cotα và giải thích vì sao ta có:
tan(α + kπ) = tanα, k ∈Z;
cot(α + kπ) = cotα, k ∈Z;
Từ ý nghĩa hình học của tanα và cotα hãy suy ra với mọi số nguyên k, tan(α + kπ) = tanα, cot(α + kπ) = cotα.