Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
c. DF = DC
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
d. AD < DC
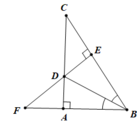
d. Trong tam giác vuông DEC có DC là cạnh huyên nên DC là cạnh lớn nhất
⇒ DC > DE mà DE = AD ⇒ DC > AD (1 điểm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
a. ∆ABD = ∆EBD
a. Hình vẽ (0.5 điểm)
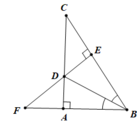
Xét ∆ABD và ∆EBD có:
∠(ABD) = ∠(DBE)
BD là cạnh chung
⇒ ∆ABD = ∆EBD(cạnh huyền – góc nhọn) (1 điểm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, phân giác BD. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng: DF = DC
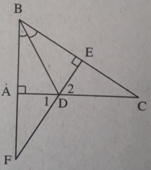
Xét ΔDAF và ΔDEC có:
DA = DE( chứng minh trên)
∠D1 = ∠D2 ( hai góc đối đỉnh)
∠DAF = ∠DEC = 90º
Suy ra: ΔDAF = ΔDEC (g.c.g) ⇒ DF = DC.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
b. BD là đường trung trực của AE
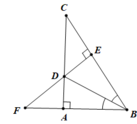
b. Ta có AB = BE ⇒ B nằm trên đường trung trực của AE (0.5 điểm)
Do ∆ABD = ∆EBD nên AD = DE (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE
Vậy BD là đường trung trực của AE (0.5 điểm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, BD là tia phân giác của góc B (D thuộc AC). Kẻ DE vuông góc với BC(E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh:a. Tam giác ABD tam giác EBDb. chứng minh DF DCc. chứng minh DADCd. gọi H là giao điểm của BD và CF K là giao điểmtrên tia đối của DFsao cho DKDF I là điểm trên đoạn thẳng CD sao cho CI2DI chứng minh rằng ba điểm K,I,H trên thẳng hàng
Đọc tiếp
Cho tam giác ABC vuông tại A, BD là tia phân giác của góc B (D thuộc AC). Kẻ DE vuông góc với BC(E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh:
a. Tam giác ABD = tam giác EBD
b. chứng minh DF = DC
c. chứng minh DA<DC
d. gọi H là giao điểm của BD và CF K là giao điểmtrên tia đối của DFsao cho DK=DF I là điểm trên đoạn thẳng CD sao cho CI=2DI chứng minh rằng ba điểm K,I,H trên thẳng hàng
Cho tam giác ABC vuông tại A, BD là tia phân giác của góc B (D thuộc AC). Kẻ DE vuông góc với BC(E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh:
a. Tam giác ABD = tam giác EBD
b. DF = DC
c. AD < DC
a) Hai tam giác = nhau theo trường hợp cạnh huyền góc nhọn (tự c/m)
b) Từ 2 tam giác = nhau ở phần a => AD= DE
Ta có tam giác ADF = tam giác EDC theo trường hợp góc cạnh góc (tự c/m)
=> DF= DC ( 2 cạnh tg ứng)
c) Xét tam giác ADF, có : góc A= 90 độ
=> DF là cạnh lớn nhất (quan hệ giữa góc và cạnh đối diện)
=> AD < DF
Mà DF= DC (chứng minh b)
=> AD < DC (đpcm)
Đúng 0
Bình luận (0)
b) Xét tam giác ADF và tam giác EDC, có:
Góc A= góc E (=90 độ)
AD= AE (vừa mình đã ns rồi)
Góc ADF= góc EDC (đối đỉnh)
Từ 3 điều trên => tam giác ADF = tam giác EDC (g-c-g)
=> DF= DC (2 cạnh tg ứng)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, tia phân giác của góc ABC cắt AC tại D, kẻ DE vuông góc với BC(E thuộc BC) , gọi F là giao điểm của BA và tia ED.
A) tam giác ABD= tam giác EBD
B)tam giác DFC cân
C) Gọi H là giao điểm của BD và CF. Trên tia đối của tia DF lấy điểm K sao cho DK=DF.Vẽ điểm I nằm trên đoạn thẳng CD sao cho CI=2DI.Chứng minh DH vuông góc với CF và ba điểm K,I,H thẳng hàng
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
=>ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D
c: Xét ΔBFC có
FE,CAlà đường cao
FE cắt CA tại D
=>D là trực tâm
=>BD vuông góc CF tại H
=>DH vuông góc CF tại H
mà ΔDFC cân tại D
nên H là trung điểm của FC
Xét ΔKFC có
CD là trung tuyến
CI=2/3CD
Do đó: I là trọng tâm
mà H là trung điểm của CF
nên K,I,H thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC (Góc A=90 độ), phân giác góc B cắt AC tại D.
a) So sánh AB và BD
b) So sánh BC và BD
c) Kẻ DE vuông góc với BC tại E. Gọi F là giao điểm của BA và ED. Chứng minh BDlà đường trung trực AE
d) Chứng minh DF=DC
e) Chứng minh AD<DC
Cho tam giác ABC vuông tại A, kẻ phân giác BD (D thộc AC), kẻ DE vuông góc với BC tại E. Gọi F là giao điểm của tia BA và ED. Chứng minh:
a) Tam giác BDA= tam giác BDE
b) DC=DF
Mik đg gấp. Ai giải đúng và nhanh mik sẽ tick cho!
a ) Xét \(\Delta\)ABD và \(\Delta\)EBD có :
BD : cạnh chungBÂD = BÊD ( = 90° )Góc ABD = Góc EBD ( vì BD là phân giác của góc ABE )\(\Rightarrow\)\(\Delta\)ABD = \(\Delta\)EBD ( cạnh huyền - góc nhọn )
b ) Xét \(\Delta\) ADF và\(\Delta\)EDC có :
AD = DE ( \(\Delta\)BDA = \(\Delta\)BDE )Góc ADF = Góc EDC ( đối đỉnh )DÂF = DÊC ( = 90° )\(\Rightarrow\)\(\Delta\)ADF = \(\Delta\)EDC ( cạnh góc vuông - góc nhọn kề )
\(\Rightarrow\)FD = CD ( 2 cạnh tương ứng )
bạn ko vẽ hình được à?
