d. Trong tam giác vuông DEC có DC là cạnh huyên nên DC là cạnh lớn nhất
⇒ DC > DE mà DE = AD ⇒ DC > AD (1 điểm)

d. Trong tam giác vuông DEC có DC là cạnh huyên nên DC là cạnh lớn nhất
⇒ DC > DE mà DE = AD ⇒ DC > AD (1 điểm)
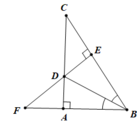
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
c. DF = DC
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
a. ∆ABD = ∆EBD
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
b. BD là đường trung trực của AE
Cho tam giác ABC vuông tại A, phân giác BD. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng: AD < DC
Cho tam giác ABC vuông tại A, BD là tia phân giác của góc B (D thuộc AC). Kẻ DE vuông góc với BC(E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh:
a. Tam giác ABD = tam giác EBD
b. DF = DC
c. AD < DC
Cho tam giác ABC vuông tại A có BE là tia phân giác của góc B ( E thuộc AC). Từ E kẻ ED vuông góc với BC tại D.
a) Chứng minh ΔABE = ΔDBE.
b) Chứng minh BE⊥AD
c) Gọi F là giao điểm của tia BA và tia DE. Chứng minh tam giác EFC cân tại E.
help pls ![]()
cho tam giác abc vuông tại a tia phân giác của góc abc cắt ac tại d kẻ DE vuông với BC tại E gọi F là giao điểm của tia BA và tia FD chứng minh tam giác DFC cân
Cho tam giác ABC vuông tại A, AB > AC . Từ B kẻ BD là tia phân giác của góc ABC (D thuộc AC). Trên BC lấy E sao cho AB = BE.
a) Chứng minh: AD = DE.
b) Gọi F là giao điểm của các tia BA và ED. Chứng minh tam giác ADF = tam giác EDC
c) chứng minh BD vuông góc với CF