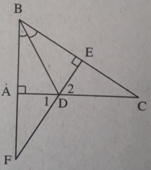
Xét ΔDAF và ΔDEC có:
DA = DE( chứng minh trên)
∠D1 = ∠D2 ( hai góc đối đỉnh)
∠DAF = ∠DEC = 90º
Suy ra: ΔDAF = ΔDEC (g.c.g) ⇒ DF = DC.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, phân giác BD. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng: AD < DC
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
c. DF = DC
Cho tam giác ABC vuông tại A; BD là ia phân giác góc B ( D thuộc AC ). Kẻ DE vuông góc BC (E thuộc BC). Gọi F là giao điểm của BA và ED .Chứng minh rằng:
a) Tam giác ABD = Tam giác EBD
b) DF = DC
c) AD < DC
cho tam giác ABC vuông tại A. BD là tia phân giác góc B. B thuộc AC , kẻ DE vuông góc BC . E thuộc DC. gọi F là giao điểm của BA và ED. Chứng minh rằng :
a) tam giác ABD bằng tam giác EBD .
b) DF = DC .
c) AD < DC
Cho tam giác ABC vuông tại A, BD là tia phân giác của góc B (D thuộc AC). Kẻ DE vuông góc với BC(E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh:
a. Tam giác ABD = tam giác EBD
b. DF = DC
c. AD < DC
Cho tam giác ABC vuông tại A, phân giác BD. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng: BD là đường thẳng trung trực của AE
Cho tam giác ABC vuông ở A, có AB = 6cm; AC = 8cm, phân giác BD. Kẻ DE vuông góc với BC (E thuộc BC). Gọi F là giao điểm của BA và ED
a) Tính độ dài cạnh BC?
b) Chứng minh DF = DC
c) Chứng minh D là trung trực của tam giác BFC
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
d. AD < DC
Cho tam giác ABC vuông tại A, kẻ phân giác BD (D thộc AC), kẻ DE vuông góc với BC tại E. Gọi F là giao điểm của tia BA và ED. Chứng minh:
a) Tam giác BDA= tam giác BDE
b) DC=DF
Mik đg gấp. Ai giải đúng và nhanh mik sẽ tick cho!