a)

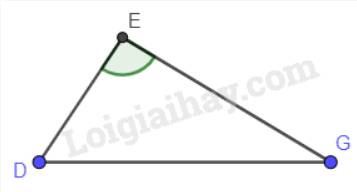
Trong tam giác DEG có góc E là góc tù (góc > 90°). Mà DG là cạnh đối diện với góc E nên DG là cạnh lớn nhất trong tam giác.

Vậy DE < DG.

b)

Tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Mà tổng ba góc trong một tam giác bằng 180°. Vậy \(\widehat P = 180^\circ  - 56^\circ  - 65^\circ  = 59^\circ \).

Ta thấy: \(\widehat M < \widehat P < \widehat N\). Hay cạnh nhỏ nhất của tam giác MNP là NP (đối diện với góc M), cạnh lớn nhất của tam giác MNP là MP (đối diện với góc N).

\(\widehat{N}=\widehat{P}=56^0\)

a) Từ điểm M kẻ đường thẳng vuông góc với AD cắt AD tại Q.

Áp dụng ĐL Pytagore cho \(\Delta\)MCN vuông ở C và \(\Delta\)MQP vuông ở Q; ta có:

CM² + CN² = MN²;  MQ² + PQ² = MP²

\(\Delta\)MNP là tam giác đều nên MN = MP. Do đó: CM² + CN² = MQ² + PQ² (1)

Dễ thấy: Tứ giác ABMQ là hình chữ nhật => AQ = BM và MQ = AB = a      (2)

(1); (2) => CM² + CN² = a² + PQ² <=> (a - BM)² + CN² = a² + (AP - AQ)²

<=> a² - 2a.BM + BM² + CN² = a² + AP² - 2.AP.AQ + AQ²

<=> CN² - AP² = a² - 2.AP.AQ + AQ² - a² + 2a.BM - BM²

<=> CN² - AP² = 2a.BM - 2.AP.AQ + (AQ² - BM²)

<=> CN² - AP² = 2a.BM - 2.AP.BM   (Do AQ = BM theo cmt)

<=> CN² - AP² = 2.BM.(a - AP) <=> CN² - AP² = 2.BM.DP (đpcm).

b) Hạ đường cao NH của \(\Delta\)MNP: 

Ta có: cos 60⁰ = \(\frac{\sqrt{3}}{2}\)=> NH = \(\frac{\sqrt{3}}{2}\).MN = \(\frac{\sqrt{3}}{2}\).MP (Vì \(\Delta\)MNP đều)

Theo quan hệ đường xiên hình chiếu: MP > MQ = a => NH > \(\frac{\sqrt{3}}{2}\).a

=> S_MNP = MP.NH /2 > \(\frac{\sqrt{3}}{4}\)a² 

Vậy Min S_MNP = \(\frac{\sqrt{3}}{4}\)a² .Dấu "=" xảy ra <=> N là trung điểm của DC và M;P nằm trên BC;AD cho ^CNM = ^DNP = 60⁰.

\(\sin60^0=\frac{\sqrt{3}}{2}\) mới đúng, bn sửa lại nhé.

Cảm ơn bạn nhiều lắm vì đây là bài thi chọn đội tuyển HSG dự thi cấp thị xã, nhờ hình vẽ của bạn mà mình đã biết cách vẽ đường phụ để hoàn thành bài, mình không biết nói gì nữa, cảm ơn bạn rất nhiều.

Gọi giao điểm của AC và BD là O
Vì ABCD là hình thang cân nên tam giác AOB cân tại O mà  ˆAOB=600⇒AOB^=600⇒ tam giác AOB đều, ta giác COD đều
Mặt khác: 
BM là đường cao của tam giác AOB nên BM cũng là trung tuyến  MA=MO
CN là đường cao của tam giác COD nên cn cũng là trung tuyến NO=ND
Tam giác AOD có: MA=MO, NO=ND 
Tam giác BMC vuông tại M có MP là trung tuyến nên \(MP=\frac{BC}{2}=\frac{AD}{2}\)
Tam giác BNC vuông tại N có NP là trung tuyến nên \(NP=\frac{BC}{2}=\frac{AD}{2}\)
Do đó: MN=NP=MP