Trong tam giác MNP có M N = 9 c m , N P = 13 c m , M P = 25 c m . Khẳng định nào sau đây là đúng:
A. P < M < N
B. M < P < N
C. N < M < P
D. P < N < M
GT: Tam giác ABC , tam giác MNP
Góc A = góc M = 90o
BC = NP
AC=MP
KL: Tam giác ABC=MNP
Mk cảm ơn
Cho tam giác MNP cân tại M , MH là phân giác góc NMP , O là trung điểm của HP
a, C/m tam giác MNP = tam giác MPH
b, C/m là trung truyến tam giác MNP
c, G là trọng tâm của tam giác MNP , MN =13 cm , NP= 10 cm . Tính MG
d,Trên tia đối của tia OM lấy điểm Q / MO=OQ.I là trung điểm của NQ . C/m M,H,I thẳng hàng
a, sửa thành tam giác MNH nhá =))
Xét tam giác MNH và tam giác MPH
MH_chung
MN = MP (gt)
^NMH = ^PMH ( vì MH là p/g )
=> tam giác MNH = tam giác MPH ( c.g.c )
cho tam giác MNP vuông tại m có N = 60 độ và MN = 7cm tia phân giác của góc N cắt MP tại D kẻ DE vuông góc vs NP tại E
a) c/m tam giác NMD = tam giác NDE
b) c/m tam giác MNE là tam giác đều
c)NP = ?
a) Xét hai tam giác vuông tam giác NMD ( M = 90 độ ) và tam giác END ( E = 90 độ ) có
ND là cạnh chung
góc MND = góc END ( vì ND là tia phân giác )
Do đó tam giác NMD = tam giác END ( cạnh huyền - góc nhọn )
b) Ta có tam giác NMD = tam giác END ( cmt )
=> NM = NE ( hai cạnh tương ứng )
Mà góc N = 60 độ
=> tam giác MNE là tam giác đều
c) Ta có tam giác MNE là tam giác đều
=> NM = NE = ME ( 1 )
=> góc NME = 60 độ
Ta có góc NME + góc EMP = 90 độ
Mà góc NME = 60 độ ( cmt )
=> góc EMP = 30 độ ( * )
Ta có tam giác NMP vuông tại M
=> góc N + góc P = 90 độ ( hai góc nhọn phụ nhau )
Mà góc N = 60 độ
=> góc P = 30 độ (**)
Từ (*) và (**) suy ra
tam giác EMP cân tại E
=> EM = EP ( 2 )
Từ (1) và (2) suy ra
NE = EP = 7 cm
Mà NE + EP = NP
7 cm + 7 cm = NP
=> NP = 14 cm
Vậy NP = 14 cm
cho tam giác MNP cân tại M có góc M = 2P. tính góc M,P,N. tam giác MNP là tam giác j. giúp mình với
góc P = 30 độ
góc M = 60 độ
ta áp dụng đl tổng 3 góc trog 1 tam giác
=> góc N = 90 độ
Vậy MNP là tam giác vuông cân .
tam giác nhọn MNP có MH , NK ,PS là 3 đường cao
a) c/m : tam giác MNP đồng dạng với tam giác MKS
b) c/m : tam giác MNP đồng dạng với tam giác HNS
c) c/m : tam giác MNP đồng dạng với tam giác HKS
a) Xét tam giác \(MKN\)và tam giác \(MSP\):
\(\widehat{M}\)chung
\(\widehat{MKN}=\widehat{MSP}\left(=90^o\right)\)
\(\Rightarrow\Delta MKN\)đồng dạng với \(\Delta MSP\)(g.g)
\(\Rightarrow\frac{MK}{MS}=\frac{MN}{MP}\)
\(\Rightarrow\frac{MK}{MN}=\frac{MS}{MP}\).
Xét tam giác \(MNP\)và tam giác \(MKS\):
\(\widehat{M}\)chung
\(\frac{MK}{MN}=\frac{MS}{MP}\)(cmt)
Suy ra tam giác \(MNP\)đồng dạng với tam giác \(MKS\)(c.g.c).
b), c) Tương tự.
Cho hai tam giác bằng nhau: Tam giác ABC và tam giác có ba đỉnh là M, N, P. Biết \(\widehat{A}=\widehat{N}\); \(\widehat{C}=\widehat{M}\). Hệ thức bằng nhau giữa hai tam giác theo thứ tự đỉnh tương ứng là:
A. △ABC = △MNP B. △ABC = △NPM
C. △BAC = △PMN D. △CAB = △MNP
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
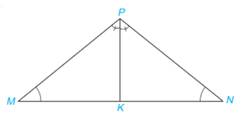
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
Cho tam giác ABC có diện tích 36cm2. Gọi M, N, P là các điểm chính giữa của các cạnh AB, AC, BC. Khi đó diện tích tam giác MNP là:
Vì diện tích tam giác = a x h : 2
nên suy ra a x h là: 36 x 2 = 72 cm
Và vì 8 x 9 = 72 và độ dài đáy (BC) nhỏ hơn chiều cao (AC)
Nên = > Độ dài đáy: 8 cm
Chiều cao: 9 cm
Vì cạnh MN = 1/2 chiều cao AC nên độ dài là: 9 : 2 = 4,5 cm
Vì cạnh PM = 1/2 độ dài đáy BC nên cạnh đó dài: 8 : 2 = 4 cm
= > Diện tích tam giác là MNP: 4 x 4,5 : 2 = 9 cm2
Đáp số.......
Câu 1: cho tam giác MHK vuông tại H ta có:
A. M+K>90o B. M+K=180o C. M+K=90o D. M+K<90o
Câu 2: cho tam giác ABC= tam giác MNP. Trong các khẳng định sau đây khẳng định nào sai:
A. B=N B. BC=MP C.P=C D. BC=PN
Câu 3: Cho tam giác PQR= tam giác DEF, trong đó PQ= 4cm; QR=6cm; PR=5cm. Chu vi tam giác DEF là:
A. 14cm B. 17cm C. 16cm D. 15cm
Câu 4: Cho tam giác ABC có góc ACx là góc ngoài tại đỉnhC của tam giác ABC. Khi đó:
A. ACx<B B. ACx=A+B C. ACx<A D. ACx=A-B
Câu 5: Chọn đáp án sai. tam giác MNP= tam giác M'N'P', MN=26cm, M'P'=7cm. Góc M=55o
A. P'=55o B. M'N'=26cm C. NP=7cm D. M'=55o
Câu 6: Trường hợp bằng nhau cạnh-cạnh-cạnh của hai tam giác được phát biểu:
A. Nếu 2 cạnh của tam giác này bằng 2 cạnh của tam giác kia thì hai tam giác đó bằng nhau.
B. Nếu 2 góc và một cạnh của tam giác này bằng 2 góc và một cạnh của tam giác kia thì hai tam giác đó bằng nhau.
C. Nếu 3 góc của tam giác này bằng ba góc của tam giác kia thì hai tam giác đó bằng nhau.
D. Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Câu 7: Tổng ba góc ngoài của một tam giác bằng:
A. 90o B. 270o C. 180o D. 360o
Câu 8: Góc ngoài của tam giác là:
A. Góc bù với một góc của tam giác.
B. Góc phụ với một góc trong của tam giác.
C. Góc kề với một góc của tam giác.
D. Góc kề bù với một góc trong của tam giác.
Câu 9: Cho tam giác ABC vuông tại A. Ta có:
A. A=B-C B. B+C=90o
C. Góc B và góc C kề bù D. Góc B và góc C bù nhau
Câu 10: Tam giác ABC vuông tại B, ta có:
A. A+C=90o B. A=45o C. B+C=90o D. B=45o
Câu 11: Cho tam giác ABC vuông tại A, phân giác BE, biết BEC=110o. Tính góc C
A. 80o B. 60o C. 70o D. 50o
Câu 12: Cho tam giác ABC và tam giác có ba đỉnh P; H; N bằng nhau. Biết AB=HN, A^=N^. Viết kí hiệu bằng nhau giữa hai tam giác
A. ΔABC=ΔNPH B. ΔABC=ΔHPN
C. ΔABC=ΔPHN D. ΔABC=ΔNPH
Cho tam giác MNP vuông tại M cóM N = 15 c m;
P N = 25 c m.
Tính số đo (làm tròn đến độ) :